[Solution]Problem 30: Find Distance to nearest Exit[Google]

Shortest Distance, Graph Traversal, Path Finding

Get hyped my amazing coders,

Let’s get into the solution for a very interesting question. Google questions can be tricky because Google loves asking questions that have an element of misdirection. They seem like they would be doable one way, but the optimal solution is something else. This is especially true for their coding challenges. When I was invited to solve Google’s notorious Foobar challenge, I noticed that all the questions had blobs of text that could make figuring out what to do much harder.

Google Foobar is a fun challenge. If you get invited to solve it, you should give it a go. The topics can get pretty out there though, so you’ll have to study up.

To learn more about my experiences with the challenge, and how I solved it, make sure you tune in for this week’s Storytime Saturday. We’re keeping this Week Google-themed. Now let’s proceed through to the solution.

Problem

This problem was asked by Google.

You are given a m x n 2D grid initialized with these three possible values:

-1 - A wall or an obstacle.
0 - A gate.
INF - Infinity means an empty room.

Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.

For example, given the 2D grid:
INF -1 0 INF
INF INF INF -1
INF -1 INF -1
0 -1 INF INF

After running your function, the 2D grid should be:
3 -1 0 1
2 2 1 -1
1 -1 2 -1
0 -1 3 4

[FREE SUBS]To buy the solution for this problem, use any of the following links. The price is 3 USD. Once you send the payment, message me on IG, LinkedIn, Twitter, or Email:

Venmo: https://account.venmo.com/u/FNU-Devansh

Paypal: paypal.me/ISeeThings

Step 1: Birds Eye View

One of the standard openers on this newsletter, we start this question by taking a step back. Let’s look at what we’ve been given and figure out some simple details. The first detail that we can hash out is the concept of distance. How are we defining it? Since we have been given a grid, it might be tempting to take the Euclidean Distance between these points. This temptation will be even stronger if, like me, you work in AI/Machine Learning and calculate distance in the context Vector Spaces.

Funnily enough, this is the most basic kind of distance in Math. It rarely comes up in coding interviews though. The distance that comes up here is closer to Manhattan Distances. We’ll go over these soon, don’t worry.

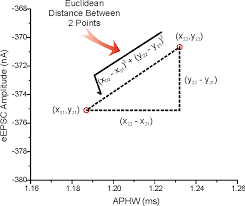
Luckily for us, they give us a sample input. Let’s bring it back here so we won’t have to scroll up.
INF -1 0 INF
INF INF INF -1
INF -1 INF -1
0 -1 INF INF

with the required output:

3 -1 0 1
2 2 1 -1
1 -1 2 -1
0 -1 3 4

Notice there is a gate at [0][2]. The location at [1][1] is said to be 2 units away. This does not align with the Euclidean Distance. Instead, the distance calculation we are using here is closer to the Manhattan Distance.

Named after the fact that a Taxi driver would have to follow the perpendicular roads when driving in Manhattan. Otherwise, they would crash into the buildings

Let’s take a look at what we have been given. We have a grid, and we want to calculate the distance of every point on that grid to the closest gate (assuming it is reachable). In other words, this distance is the primary relationship between two points (location and the gate). Now is there a relational data structure that we can use to encode such relations?

Enter the Graph

Most resources online tend to focus on what Graphs are. They typically tell you that Graphs are defined by a set of vertices and a set of edges connecting the vertices. This is true, but not very useful if you want to use it. Here is a better way to think about Graphs: Graphs are data structures that represent relationships between objects.

Nodes: Our objects. Edges just become a way to show that there is a relationship between our objects.

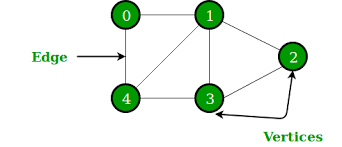
Let’s take a look at an example, specific to this question. Here we have different locations (of walls, gates, and rooms). And we want the distance between these various locations. Here the location (given by index on the grid) becomes our node, and the manhattan distance between locations becomes our edges. Since we only care about distances from rooms to nearest gates, we will only create those edges. Take a second to pause, and make sure our rationale for using a graph and method for building one makes sense.

This is checkpoint number one. Only proceed if you have fully understood everything.

I have no doubt that my more advanced subs (especially those that are currently working with me), had identified this as a graph problem. And I could have directly said use a graph here, which is what coding blogs/tutorials/videos and even premium services do. However, that would not be useful to anybody. Graphs are a beautiful and elegant data structure, and I want you to be able to use them to their full extent. There is a reason companies like Spotify, Netflix, and YouTube all use Graphs heavily (I will cover it soon. To not miss it, make sure you are following me on LinkedIn and Medium). They are unfortunately not taught properly, so people miss out on their complete awesomeness. I will make sure that this doesn’t happen to the readers of my content.

Graphs are some of the most important Data Structures. However, most people are never taught to appreciate them.

Let’s get back to the question on hand. We have now identified that this problem can be solved with graphs, and how we should set up our graphs. Now the next step is how do we traverse this graph to calculate the distances. There is always DFS (Depth-First Search) and BFS (Breadth-First Search). We could get fancy with A*, Djikstra, or Bellman-Ford. How can we pick the best traversal algorithm for our question?

If this is something that confuses you, make sure you check in for Math Mondays. Next Monday, I will cover the important path-finding algorithms in detail. For now, I will just use the spark notes version.

Step 2: Picking the best graph traversal algorithm

It can be a little overwhelming to find the best algorithm in graph traversal. There are very subtle nuances b/w them which make choosing hard. Let’s go over it here.

The first thing that we can notice is that this graph is not weighted. The distance between points (0,0) and (1,0) will always be equal to the distance between (2,3) and (2,4). This goes back to the Manhattan distance. This means that we can use a simple algorithm like BFS over the more complex path-finding algorithms (which shine in graphs with unequal weights). To understand take a simple example.

The different colors represent different slopes and landscapes.I actually did this kind of contouring Path Finding AI for one of my projects in college

Imagine you were developing a running path creator. If you were running on identical terrain throughout, you would only care about the distance b/w two points. 1KM traveled on any path would take identical amounts of energy. However, now imagine your terrains could change (swamps, mud, water, slopes etc). Running 1KM on a plain would be very different than 1KM through a swamp.

For the first kind of AI, a BFS would be great. For the second, more comprehensive planner, we want to use a better and more comprehensive pathfinding algorithm, that can account for differing weights. That should make it clear why we are using a BFS for this particular problem.

A classic meme. Subscribe for the GIFs and memes.

You might be wondering I haven’t mentioned DFS yet. If you look online, lots of people try to solve this problem with a DFS. However, DFS is not a good pathfinding algorithm. This is because with DFS if the algorithm goes down the wrong path, it will waste a lot of time before returning. And if it does go down a path that is non-optimal, it will simply return that path. So trying DFS in a path-finding context is not a smart idea. Unlike BFS, DFS is not guaranteed to return the optimal path (and in some cases, might never terminate). This is Djikstras, A*, and other pathfinders are based on BFS. This is why we will use BFS to solve this problem.

However, there is a twist. And that twist is why this problem is so brilliant (and the reason I selected it for this week). Using this simple twist, we will be able to solve this question in a really neat and efficient way. Let’s discuss what it is.

Step 3: Multi-Source BFS

You will notice something interesting, we have multiple gates. Multiple gates imply multiple possible sources. The standard approach would be to pick a gate and run BFS to all rooms. We update the values at all indexes accordingly. Then we do this for another gate, changing the value at an index when the distance we calculate is lesser than the current distance calculated. Continue to do this for all the gates.

However, this approach is terrible. The time complexity of such a solution would be O(g*m*n) where g is the number of gates in our grid. This is because, in every BFS, we will visit every location in the grid. This is an O(m*n) operation. Since this operation would be repeated g times (for every gate), the overall complexity will become O(g*m*n).

So …how can we improve this?

BFS goes level by level. There is no reason we can’t add multiple nodes (gates) to the first level. There’s your hint. Try to work this out for yourself before proceeding

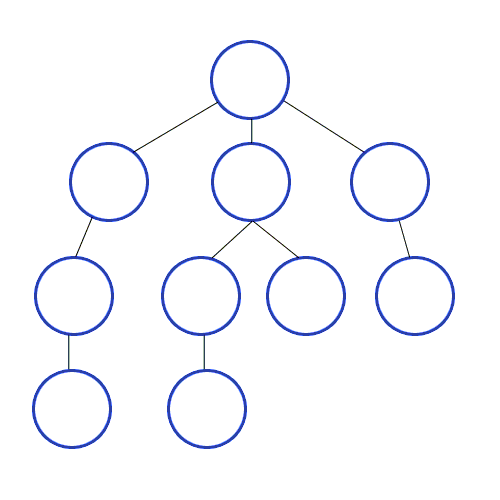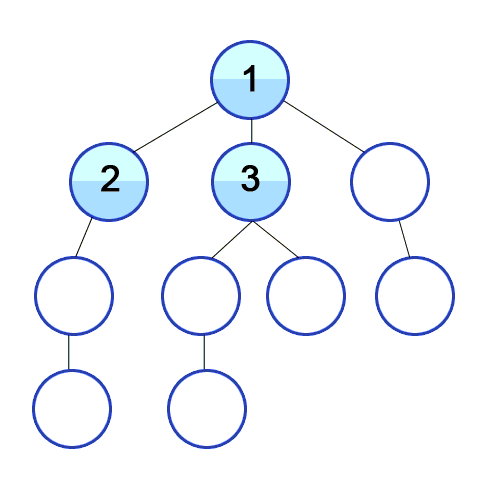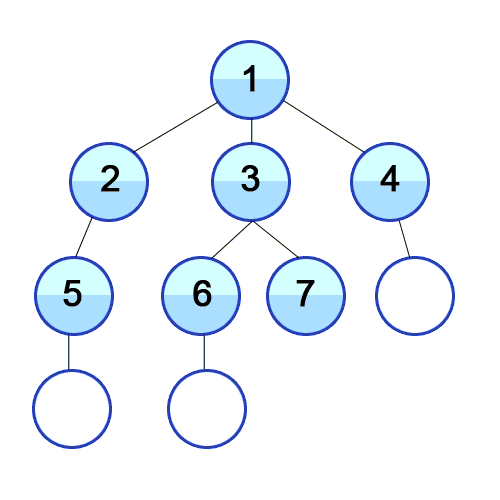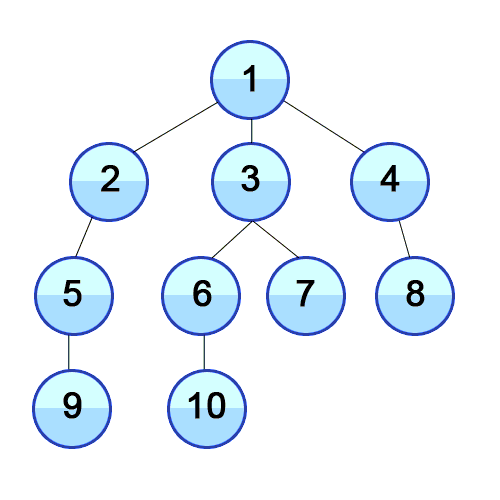
I want you to notice something. For any given empty room, there is only one possible closest gate. If it is equidistant to more than one, we can select any gate.

We can take advantage of the layer-by-layer nature of BFS to put this insight to use. Traditional BFS starts with a single source i.e, a single node at level 1 (distance 0). Let’s look at the logic for BFS for distance mapping

Initialize queue Q
Initialize array d[N] = [INF]*len(Nodes) #for distances from source
Q.enqueue(a)
distance = 0
d[a] = 0
while Q is not empty:
  n = Q.dequeue
  distance = distance + 1
  for each neighbor n_i of n:
    if d[n_i] is infinity:
      d[n_i] = distance
      Q.enqueue(n_i) 

Notice that this will automatically traverse and assign the correct values for distances to one source. If we tweaked the code a little bit to accommodate the starting sources, then we should be to traverse all the distances without major problems.

One final consideration is how we account for the walls and obstacles. We can keep it simple. If something is not INF (empty room not visited), we will not add it to our queue. Thus a room surrounded by walls will never be reached and will never have its value changed (which is what we want). If it is only reachable through 1 free neighbor, it will only be added after that room, which makes sense.

We are finally near the end. Let’s put everything together for our solution

Step 4: Final Solution

The code we can use to finish this problem looks like this:

 def wallsAndGates(self, rooms):
        """
        :type rooms: List[List[int]]
        :rtype: void Do not return anything, modify rooms in-place instead.
        """
        wall = -1
        gate = 0

        if not rooms or not rooms[0]:
            return

        numRows = len(rooms)
        numCols = len(rooms[0])

        currLevel = []

        for i in range(numRows):
            for j in range(numCols):
                if rooms[i][j] == gate:
                    currLevel.append( (i,j) )

        while currLevel:
            nextLevel = []
            for i,j in currLevel:
                currDist = rooms[i][j]

                for nextI,nextJ in [(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:
                    if 0<=nextI<numRows and 0<=nextJ<numCols and rooms[nextI][nextJ]==float('INF'):
                        rooms[nextI][nextJ] = currDist + 1
                        nextLevel.append( (nextI,nextJ) )

            currLevel = nextLevel

Notice a few things. We initialize the q with all the gates before the BFS starts. Our neighbors are defined as Right, Left, Up, Down (in accordance with our observations about distance). Now let’s discuss the complexities

Time Complexity- O(n*m) because we visit each node once

Space Complexity- O(n*m). This will occur when we have every room 1 distance away from a gate, so we add everything to the list. Also happens if every location passed in the grid is a gate.

Make sure you share your thoughts on this question/any interesting questions/developments in the comments or through my links.

Happy Prep. I’ll see you at your dream job.

Interview Ace,

Devansh <3

Reach out to me on:

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75