[Solution]Problem 11: Counts nodes in Complete Binary Tree [Amazon]

Easy

Problem

This problem was asked by Amazon.

Given a complete binary tree, count the number of nodes in faster than O(n) time. Recall that a complete binary tree has every level filled except the last, and the nodes in the last level are filled starting from the left.

Solution

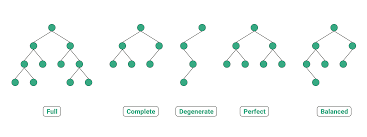
If we didn’t have any time restrictions, we could just go to every node and keep track of the count. But that doesn’t work since the solution would be linear time. We need to go faster. Look at the following image with trees to see the common types of trees.

Now that we understand trees, how do we get faster?

If you look at the thread about how to solve most tree questions (

https://codinginterviewsmadesimple.substack.com/p/ways-to-solve-most-tree-question/comments) you will see the following breakdown for a generic tree solution:

def treeFunc(root, **other params):
    if(root==null):
        return baseCase/other relevant params
    val=operation(treeFunc(root.left), treeFunc(root.right))
    return val

How does this apply to our question/solution? We know that the number of nodes in a tree= root + number of nodes(root.left) + number of nodes(root.right). See how we can fit that into our template? Now we go onto the next steps.

Using what we got

Remember we are given a specific condition. Our input is always a complete binary tree. This also means that we are given some conditions that we can use. A complete binary tree can split into two distinct sub-trees. One of these trees is guaranteed to be full. The other may be full (we have a full tree). Or we have another complete binary tree. See the magic?

We can keep cutting out the subtrees that are not full in logarithmic time. Eventually, we will get to the last layer, where we can count directly. And what about the full binary (sub)trees? That’s where we use some math.

For a full tree, the depth to the leftmost node is the same as the depth to the rightmost node, and the number of nodes is 2^(depth+1)- 1. In other words, in this case, using only two O(h) operations, we can calculate the total number of nodes. As a result, whenever we find a complete subtree, we can calculate its node count directly and stop recursing. And because this is a complete tree, it must be the case that either the left or right subtree (or both) is full, at each level. In this way, we will only need to analyze half the tree at each depth.

And what of the not full binary trees? Simple we can just…

split them. Since we have the property that the subtree will split into a full and complete (sub)sub-tree. We can keep calculating the trees using the following code:

def find_left_height(root):
    height = 0
    while root.left:
        root = root.left
        height += 1
    return height

def find_right_height(root):
    height = 0
    while root.right:
        root = root.right
        height += 1
    return height

def count_nodes(root):
    if not root:
        return 0
    left = find_left_height(root)
    right = find_right_height(root)

    if left == right: #(sub)tree is full
        return (2 << left) - 1
    else:
        return count_nodes(root.left) + count_nodes(root.right) + 1

Sketch through a few examples to convince yourself why this would work. Otherwise, just reach out to me for an explanation.

What about time complexity? At each level of the tree we make a constant number of O(h) calls, where h is the depth at that level. So our time complexity is O(h + (h - 1) + ... + 0) = O(h^2) = O((log N)2).

Bonuses/Promotion (Get Free Stuff)

Have anything to say to me? Use the links below.

To learn how to interview better DM me. Let’s set up mock interviews and go over different interview techniques. In addition to focused questions, and a detailed personalized plan, we will go over the right questions to ask during your interviews.

To share interesting problems/solutions with me, reach out to me. Different social media of mine also have other content from me. Good problems and/or solutions receive a free shoutout + 2 months of the paid newsletter:

Reach out to me on Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/