[Solution]Problem 19: Help Couples sit together [Spotify]

Recursion. Branching, Combinatorics, Couples, Rearragment

Problem

This problem was asked by Spotify.

There are N couples sitting in a row of length 2 * N. They are currently ordered randomly but would like to rearrange themselves so that each couple's partners can sit side by side.

What is the minimum number of swaps necessary for this to happen?

Brute Force

The clearest thing we can do here is to create our brute force solution. Brute force solutions can point us in relevant directions to come up with the optimal solution.

Suppose the couples are labeled (0, 1), (2, 3), (4, 5), ...,(n-1, n) and they are sitting on consecutive couches in the following arrangement: [(0, n), (1, n-3), (2, n-6), ...].

Then for the first pair, there are two ways to make a swap such that a couple will end up together on the first couch. That is, we can either swap person 0 with person n-3, or swap person n with person 1.

For either option, we have possibly two options for creating a couple on the second couch, and then possibly two options for creating a couple on the third couch, and so on. Even though there are eventual cases where we have a couple already sitting on a bench, we will on average have two options/unordered pair. This concept is called the branching factor. The branching factor is the number of children at each node, the outdegree. Note that if this value is not uniform, an average branching factor can be calculated. We use branching factors to calculate the time and space complexity of our algorithms (think of how).

In our code, we could recursively go through each of these options, tracking the total number of swaps, and at the end return the minimum. Write this code out and post in the comments below for a code review. We will not write it out, because in your interviews you should ideally not waste time on such solutions if you have a better one. You want to let the interviewer know that you know the idea behind the brute force, mention the time and space complexity, and move on to a better solution.

In our case, this would take O(2^N), since we branch off into two paths at every couch. We also use O(2^N) space, since each time we branch we create two new rows.

A Better Solution

Surely there’s a better solution than just brute-forcing it. If you’re anything like me, you might try some combinatorial mathematics. However, given that we’re dealing with random configurations, this will not work. The second option would be attempting to write Monte Carlo simulations. This approach is viable in Data Science, but generally not suggested in coding interviews

A good example of Monte Carlo Methods

Let’s take a look at our solution. You will notice one thing: At worst, one swap will fix one couple as in (0, 1), (n-1, n-3),…. We can’t do any better than choosing the first person from the pair, finding the position of their partner, and swapping the second person with their partner. On average this will fix one couple’s seating. In rare cases, two couples will be fixed.

Greedy Algorithm to maximize sum of nodes vs Optimal Method

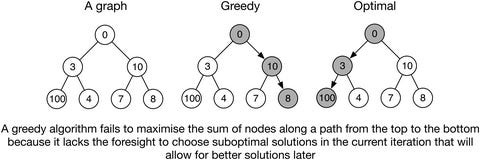
Greedy algorithms are simple, intuitive algorithms that are used in optimization problems. The algorithm makes the optimal choice at each step as it attempts to find the overall optimal way to solve the entire problem. However, since they don’t look ahead, they might be short-sighted and miss out on the best ways.

In our case, greedy algorithms will allow us to be optimal because of the properties we derived. So what would our algorithm look like? What kind of time/space complexity will it have? Think for a second before proceeding.

Our greedy algorithm, then, will simply go through each pair in the list and perform this swap if the pair does not already consist of a proper couple.

def min_swaps(row):
    n = len(row)

    positions = [0 for i in range(n)]
    for i in range(n):
        positions[row[i]] = i

    swaps = 0

    for i in range(0, n, 2):
        if row[i] // 2 == row[i + 1] // 2:
            continue

        if row[i] % 2 == 0:
            partner = positions[row[i] // 2 * 2 + 1]
        else:
            partner = positions[row[i] // 2 * 2]

        row[i + 1], row[partner] = row[partner], row[i + 1]
        swaps += 1

    return swaps

This solution is O(N) in both time and space.

Time Complexity: O(n) Space Complexity: O(n)

Bonuses/Promotion (Get Free Stuff)

Have anything to say to me? Use the links below.

To learn how to interview better DM me. Let’s set up mock interviews and go over different interview techniques. In addition to focused questions, and a detailed personalized plan, we will go over the right questions to ask during your interviews.

For most of my students, mock interviews have been very helpful. Enough mock interview practice is the key between getting that job offer and rejection. If you can get three people to become paying subscribers to this newsletter, you win a free mock interview. This offer has no upper limit, so the more subs you can get, the more mock interviews you win.

To share interesting problems/solutions with me, reach out to me. Different social media of mine also have other content from me. Good problems and/or solutions receive a free shoutout + 2 months of the paid newsletter:

Reach out to me on:

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75