[Solution]Problem 25: Boolean Satisfiability[Dropbox]

Boolean Satisfiability Problem, Boolean Algebra, Recursion,

Following is a solution that was shared with all my premium subscribers. To make sure that you don’t miss such high-quality solutions, join the crew and become one of the premium subscribers of this newsletter.

Problem

This problem was asked by Dropbox.

A Boolean formula can be said to be satisfiable if there is a way to assign truth values to each variable such that the entire formula evaluates to true.

For example, suppose we have the following formula, where the symbol ¬ is used to denote negation:

(¬c OR b) AND (b OR c) AND (¬b OR c) AND (¬c OR ¬a)

One way to satisfy this formula would be to let a = False, b = True, and c = True.

This type of formula, with AND statements joining tuples containing exactly one OR, is known as 2-CNF.

Given a 2-CNF formula, find a way to assign truth values to satisfy it or return False if this is impossible.

Step 0: Understanding the background

This can be a very confusing problem to understand. And for good reason. This question is like a very specific version of the Boolean Satisfiability Problem. The (general) SAT problem is one of the hardest problems in Computer Science and is still unsolved. It’s so important that finding an efficient solution for it will actually give you a million dollars and turn you into a bonafide rockstar. It will also be a breakthrough in many fields.

If any of you solve this problem, make sure you remember me

Fortunately, this particular version of the problem (called 2SAT) is solvable efficiently. It is just really tricky. I selected this problem because it can teach us a lot about framing the solution the right way. With this context out of the way, let’s start the solution

Step 1: Breaking down the components

With hard problems like this, it can be very easy to get caught up by all the components and details. The best way to counteract this is to just simply break down the different components of the problems. Then we simply have to state the problem statement in simple words.

Let’s do that for this problem:

1. We have a logical statement. That statement is made up of an arbitrary number of variables (a,b,c …) and their negations(¬a,¬b,…). We’ll collectively refer to the vars and their negations as literals. Our literals are boolean in nature (they can be either true or false).

2. The statement given follows a particular structure. The structure is as follows: we take 2 literals and connect them with an OR. Let’s call this a tuple. Our statement is a bunch of tuples all chained together by ANDs. This is the 2-CNF form.

3. We want to assign our literals values in a way that is consistent (a and ¬a can’t both be true) and in a way that our overall statement is true. Or we return False.

Some of you may be tempted to skip this step. But don’t do that. There are several advantages to doing this. Firstly this kind f reframing allows you to eliminate any misunderstandings, during the interview. It might also allow you to extract hints from your interviewers. It is also a phenomenal way to show off your communication and coherence. And the best part is, the more you do this, the better you will become.

Reductionism can help you a lot in your interviews. By reframing problems, you are employing reductionism

Lastly, reframing will let you gain some insight into solving the problem. For example, the question doesn’t explicitly mention that literals had to be consistent. And while it may seem obvious when I state it explicitly, this insight will actually help us solve the problem.

Step 2: Boolean Algebra

Time to get a little Mathy. The second we see OR statements between two literals, we also know that we can derive logical implications between them. In fact, a—>b (a implies b) is equal to ¬a OR b. Let’s remember that.

P→Q === ¬P∨Q

Implication Definitely messes with a lot of people. It is something you should know for handling Boolean-based questions.

Now is when we turn on the math to the next level. We might have a tuple (x OR y). That can be converted into the following statement (this is crucial to make sure you follow this step).

(¬x -> y) AND (¬y -> x) (if one of the two variables is false, then the other one must be true).

Why are we doing all this? I’m about to blow your mind

Step 3: Implication Graphs

Once we convert our tuples into this new form, we can work some magic. Implications are kinds of relations. Therefore if a—>b then we can draw a directed graph where we have an edge from a to b.

The document: https://www.tau.ac.il/~safra/Complexity/pdf/2SAT_Handouts.pdf is a pretty good crash course on the theory

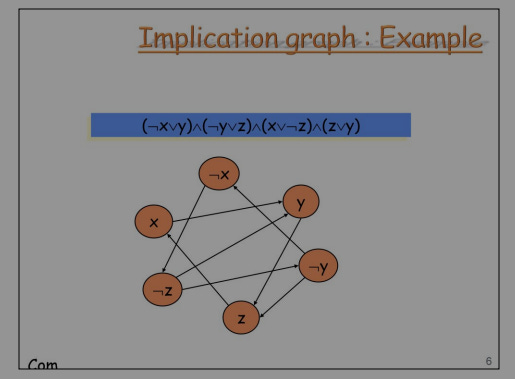
The statement above is (¬x OR y) AND (¬y OR z)AND (¬z OR x)AND (y OR z). Using the fact that (¬x or y)==(x -> y) AND (¬y -> ¬x)

We can turn our given statement into:

[(x -> y) AND (¬y -> ¬x)]AND [(y -> z) AND (¬z -> ¬y)]AND [(y -> z) AND (¬z -> ¬y)]AND [(¬y -> z) AND (¬z -> y)]

The statement is represented by the image above.

So …what does this do?

When we have a graph, we end up with a pretty cool property. Let’s say that you started at the vertice x and you could follow the edges to reach ¬x. And you could start at ¬x and reach x. Then you know that your graph (and therefore your statement) has no solution. We can return False.

We’re finally getting close to the solution.

This might have you tempted to simply run a DFS and test for reachability that way. And that is a solution. It is just not the optimal solution. For that, we want to get into some graph theory. We’re going to discuss one of the most important concepts in Graph Theory for Coding Interviews. So make sure you’re following along so far.

Step 4: Strongly Connected Components

We already said that for there to be a solution if for any variable x, we find that both x and ¬x are reachable from each other. Another way to say this would be if x and ¬x are in the same strongly connected component, then the graph has no solution.

All a strongly connected comp means is that the vertices in the same comp are reachable from each other.

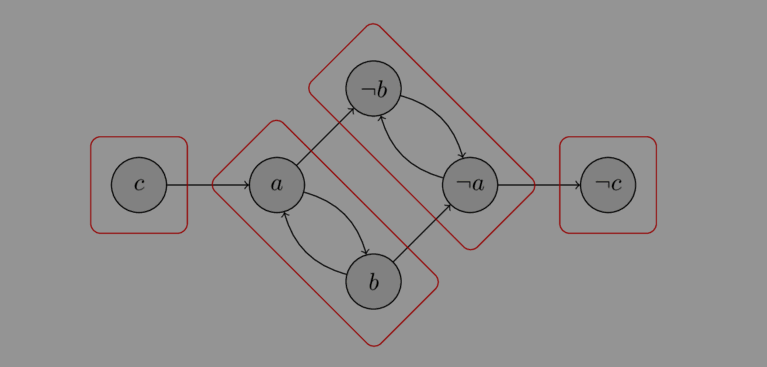
Thus, we just need to find all the SCCs (and validate that x and ¬x are in different comps). For this, we can use Kosaraju's algorithm, which visits the transpose of our graph in the topological order sorted using a depth-first search. Each component will have an associated value, where lower values signify "earlier" components.

def dfs1(node, graph, visited, order):
    visited.add(node)

    for next_node in graph.get(node, []):
        if next_node not in visited:
            dfs1(next_node, graph, visited, order)

    order.append(node)

def toposort(graph):
    order = [] 
    visited = set()

    for node in graph: 
        if node not in visited: 
            dfs1(node, graph, visited, order) 

    return reversed(order)


def get_transpose(graph):
    transpose = defaultdict(list)

    for key, values in graph.items():
        for v in values:
            transpose[v].append(key)

    return transpose

def dfs2(node, graph, visited, components, i):
    visited.add(node)

    components[node] = i

    for next_node in graph.get(node, []):
        if next_node not in components:
            dfs2(next_node, graph, visited, components, i)

def get_connected_components(graph, order): 
    transpose = get_transpose(graph)
    visited = set()
    components = defaultdict(list)
    i = -1

    for i, node in enumerate(reversed(order)):
        if node not in visited:
            dfs2(node, transpose, visited, components, i)

    return components

Finally, we are ready to solve this problem. If for any variable, we find that both x and ¬x are in the same component, this means that they imply each other, so no solution is possible.

Otherwise, we will assign each variable the truth value with the larger value in our components dictionary.

We can link this all together:

def negate(x):
    if x[0] == '¬':
        return x[1:]
    else:
        return '¬' + x

def satisfy(variables, *args):
    graph = defaultdict(list)

    for a, b in args:
        graph[negate(a)].append(b)
        graph[negate(b)].append(a)

    order = toposort(dict(graph))
    transpose = get_transpose(graph)
    components = get_connected_components(transpose, order)

    if any(components[v] == components[negate(v)] for v in variables):
        return False
    else:
        return set([max(v, negate(v), key=lambda x: components[x]) for v in variables])

Topologically sorting the graph and finding the SCCs both rely on DFS, which takes O(V + E) time. The code will thus run in O(N + M) where we have N literals with M clauses.

The graph and its transpose will each need to store all variables as keys, so we will require O(N) space as well.

PS: Don’t worry about remembering everything about this problem. Most likely you will not be expected to give the full solution. Instead, focus on how we got to the implication graph and identified the SCC rule. Also, make sure you can implement the DFS algorithm.

I created Technology Interviews Made Simple using new techniques discovered through tutoring multiple people into top tech firms. The newsletter is designed to help you succeed, saving you from hours wasted on the Leetcode grind. I have a 100% satisfaction policy, so you can try it out at no risk to you. You can read the FAQs and find out more here. Use the button below to get 20% off for upto a whole year.

Before proceeding, if you have enjoyed this post so far, please make sure you like it (the little heart button in the email/post).

Reach out to me on:

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75