[Solution]Problem 29: Arranging Coins in Staircase[Netflix]
Lists, Math, Dynamic Programming, Recursion
How’s it grooving my favorite coders,
Time to go over the solution to the problem discussed yesterday. Hope you’re excited. This post/email will be very interesting because along with the answer, we will actually be discussing some pretty interesting things related to time complexity.
Problem
This problem was asked by Netflix.
You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.
Given the integer n, return the number of complete rows of the staircase you will build.
For example, given n=5 you will return 2.
[FREE SUBS]To buy the solution for this problem, use any of the following links. The price is 3 USD. Once you send the payment, message me on IG, LinkedIn, Twitter, or Email:
Venmo: https://account.venmo.com/u/FNU-Devansh
Paypal: paypal.me/ISeeThings
Step 1: Input and Outputs
A staple approach of this newsletter, the first thing we will cover is the analysis of what exactly this question is asking. It will help us find hints about the solution, spot nuances, and allow us to analyze our performance at the end. Let’s begin our analysis.
Input—> We get an integer n. Since n is supposed to be the number of coins, we know it is non-negative (unless we want to allow debt!!!). Can it be 0? Ask the interviewer these questions. Such clarifying questions are low-hanging fruit. Always pluck the low-hanging fruit.
Output—> We want to return the maximum number of complete rows we can create. This means two things. We can’t always return 0 (we can always create 0 rows) and call it a day (this might seem silly, but paying attention to wording is very important). More importantly, we want to truncate whatever calculation we do at the end. This will make sure we always get the correct number.
This process is very simple for this problem. So it won’t take more than 2 minutes (at most). However, it is important to do as a way to drill the habit in. Now let’s work out the solution
Step 2: Looking at the staircases
We are given a pretty interesting condition. We know that the ith row will contain i coins. This tells us two things. Firstly, to complete the ith row we need to have atleast n coins left. Secondly, once let’s say we have completed i rows. This means that up to this point, we have used (1+2+3…+i) coins. Simple math tells us that we will therefore have n-(1+2+3…+i) coins left.
The simple approach would be something like this:
row,i=0,0
while n>=i{
n-=i
i+=1
}
return i Obviously if n==0 then we want to return 0.
This approach is going to be close to square root(n). Why not linear? Because, as i grows, the value of n will reduce even faster. We will cover the rationale for this on a Math Monday, so make sure you check in for them. How can we improve this? By doing some simple simplifications
Step 3: Enter the simple Math
We have already come up with the rule that when i rows have been completed, we have n-(1+2+3…+i) coins left. We also know that for every n, we will have a maximum number of rows we can complete. Let’s call that number m.
We know that numerically speaking, we have the following relationship:
n= (1+2+3…+m) + leftover coins. (Equation 1)
Since we care only about the number of complete rows, we can ignore the leftover rows. The new equation becomes
n>= (1+2+3…+m) (Equation 2).
Nothing too revolutionary so far. Time for me to blow your minds.
In math, there is a very famous equation. It is very useful for simplifying a lot of tedious calculations and will help you a lot in your developer interviews/roles.
It states that the sum of integers from 1 to any int m will be equal to-
(1+2+3…+m) = m*(m+1)/2
We will cover it on Math Mondays soon, so I won’t go too deep into it now. Here is a simple visual proof to explain the idea for now.
We can put our newfound identity into Eq. 2. This will give us:
n>=m*(m+1)/2, which we rearrange into
m^2 + m -2n=0 (since we are only dealing with complete rows, we can discard the > condition).
So how do we proceed from here?
The Quadratic Formula
Believe it or not, we’re almost done. There is a neat math trick that you can use to solve this equation directly. That is called the Quadratic Formula. It’s a pretty useful formula, but might not always show up in your interview. This is why we won’t go into details, but I would suggest remembering the formula for your own usage.
Let’s transpose m^2 + m -2n=0 into this form. We would get
a=1, b=1, and c=-2n (remember that n is an input and is constant).
Therefore, m= ( (-1 + (1+8*n)**0.5 )/2 ).
That’s it. In code form, we get this
import math
def arrangeCoins(self, n: int) -> int:
return int((-1+math.sqrt(1+8*n))/2) See how simple it becomes? Since we are doing mathematical operations, this will be constant time and space.
Time- O(1) because of the math.
Space- O(1) to store the solution.
A note on the Time Complexity of Square Root Function
Some of you that have a theoretical background might be scratching your heads. And you would theoretically be somewhat correct. There is no way to calculate the square root of an arbitrary number in constant time.

However, this is where software development is different from theoretical CS and Math. Most processors/languages have built-in optimizations to compute common functions like square root very quickly. You can find the details in the discussion linked above.
This is why keeping up with all these developments is important. This newsletter will continue to share any important information, so make sure you read regularly.
Make sure you share your thoughts on this question/any interesting questions/developments in the comments or through my links.
Reach out to me on:
Instagram: https://www.instagram.com/iseethings404/
Message me on Twitter: https://twitter.com/Machine01776819
My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/
My content:
Read my articles: https://rb.gy/zn1aiu
My YouTube: https://rb.gy/88iwdd
Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75



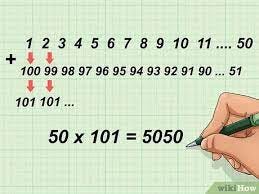

Hi,Devansh,thanks for your amazing newsletter. Btw,in the step 2,the function should return i-1 right?to return the no. of completed rows.
Also,do you have any discord/slack channel for your subscribers?