[Solution]Problem 32: Maximize Average Pass Ratio[Goldman Sachs]

Math, Problem Solving, Linear Data Structures, Lists

I hope you’re ready for this one, we’re going to learn a lot in this solution.

Problem

There is a school that has classes of students and each class will be having a final exam. You are given a 2D integer array classes, where classes[i] = [passi, totali]. You know beforehand that in the ith class, there are totali total students, but only passi number of students will pass the exam.

You are also given an integer extraStudents. There are another extraStudents brilliant students that are guaranteed to pass the exam of any class they are assigned to. You want to assign each of the extraStudents students to a class in a way that maximizes the average pass ratio across all the classes.

The pass ratio of a class is equal to the number of students of the class that will pass the exam divided by the total number of students of the class. The average pass ratio is the sum of pass ratios of all the classes divided by the number of the classes.

Return the maximum possible average pass ratio after assigning the extraStudents students. Answers within 10-5 of the actual answer will be accepted.

Example 1:

Input: classes = [[1,2],[3,5],[2,2]], extraStudents = 2
Output: 0.78333
Explanation: You can assign the two extra students to the first class. The average pass ratio will be equal to (3/4 + 3/5 + 2/2) / 3 = 0.78333.

The solution we will be discussing tomorrow

This question can be practiced as Leetcode 1792. Maximum Average Pass Ratio. Feel free to test your solution there

[FREE SUBS]To buy the solution for this problem, use any of the following links. The price is 3 USD. Once you send the payment, message me on IG, LinkedIn, Twitter, or Email:

Venmo: https://account.venmo.com/u/FNU-Devansh

Paypal: paypal.me/ISeeThings

Or you can sign up for a Free Trial Below -

Step 1: Getting all the pieces on the board

All the consistent readers know that I stress this step a lot. Understanding the question, the data given, what is needed, and the constraints are crucial for solving the problems given to us. This step also helps make relevant steps and is a great way to show off your communication and problem-solving skills.

To learn more about how to develop these skills, check out this article. 4 things to master for your coding interviews

Getting to this question, what are the important things we care about-

1. Input- classes is a list with the shape [class0, class1 …class_n]. Each class member is further a list of size 2 shaped, [pass_i, total_i]. As we know the first represents how many students will pass, and the second represents the total population of the class. We also have an int giving us a bunch of students not affiliated to any class, that we want to add to meet our objective.

2. Objective- We want to maximize the average ratio of people passing. We achieve this by strategically allocating the extra genius students to the class they will impact the most.We can calculate the ratio for a class with class[0]/class[1]

3. Interesting point to note- As we add a genius to a class, the ratio changes. Thus we want to utilize a data structure that will allow for easy retrieval and insertion.

Doing this step might seem trivial, but trust me it has a lot of benefits. You will reduce the number of mistakes you make by following this approach, and this will give you a direction to move your solution into next. Looking at all we’ve been given and all we know, we can deduce that a reasonable next step would be to figure out which class we want to add our genius to.

The answer is actually really obvious. We will add the genius to the class that would be most impacted the most. Surprising I know.

I’m sure you’re all blown away by my brilliant answer. Feel free to take a breather.

So now we have another question? How do we figure out which class has the most to gain from adding a single genius? Once we can create a function to calculate this, we can just loop till we run out of geniuses.

It might seem like this process just shifted goalposts. However, that would be incorrect. Notice how we have significantly narrowed the scope of what our next step has to be. Our minds are not good at solving big, complex, ambiguous problems. It is, however, fantastic at solving specific well-defined problems. And we now have a very useful subproblem to solve. How do we define gain?

Make sure you’re not slowing down your growth and career by missing out on the solutions.

Step 2: Defining the Gain

If you struggled with this question, I’m willing to bet that this is what you struggled with. Even if you didn’t realize it. Don’t worry this is very common. As you get more practice and interact with the newsletter more, you will get better at this.

So how do we define the gain? The hint is in the question. We know that we want to maximize the average pass ratio across classes. The obvious conclusion is to find the class that has the most to gain and add a genius to it. Once we do so, we are good. The observant among you will once again notice something. In our statement we have two subproblems i)Figure out how we quantify a class’s gain, and ii)Find the class with the highest gain. Let’s solve (i) first.

The average ratio of any class is simply numPass/numClass. This is true regardless of whether we added the genius or not. To figure out how much a class gains from adding a genius we can thus do a simple calculation

   gain= (class[0]+1)/(class[1]+1)- class[0]/class[1] 

This represents the change to the ratio passing if a genius is added. Let’s elaborate this with an example. Imagine we had a class with-

class=[1,2] #1 passing out of 2. 
gain= 2/3 -1/2= 1/6  

We can mathematically prove that adding 1 to both the numerator and denominator of a fraction increases its value (as long as it is lesser than 1). This is because we can write fractions as (d-m)/d where d,m are ints. As we keep adding 1s in both places, the difference of m stays constant. However, the missing m is a lower proportion of the number. The difference of 1 in 1/2 is huge. The difference of 1 in 99999/100000 is negligible.

For my ML peeps, especially, Limits are a very important concept. We will cover them soon.

Now comes the next part of the question. We already have how to calculate the gain. It is tempting to call it quits here. We can simply try to sort our list based on this prospective gain, pop the one with the highest gain, add our value and use insertion sort to insert it into the list. Since we have already sorted our list once, insertion sort would be relatively cheap. But it can fail. Think of cases where we have a lot of classes and ratios are relatively close. We can use binary search to identify ideal locations, but this would be a hassle. Is there a better way?

Step 3: Going back to the Start

Remember the interesting observation we made? All the way at the start? Don’t scroll up, I’ll paste it here

As we add a genius to a class, the ratio changes. Thus we want to utilize a data structure that will allow for easy retrieval and insertion.

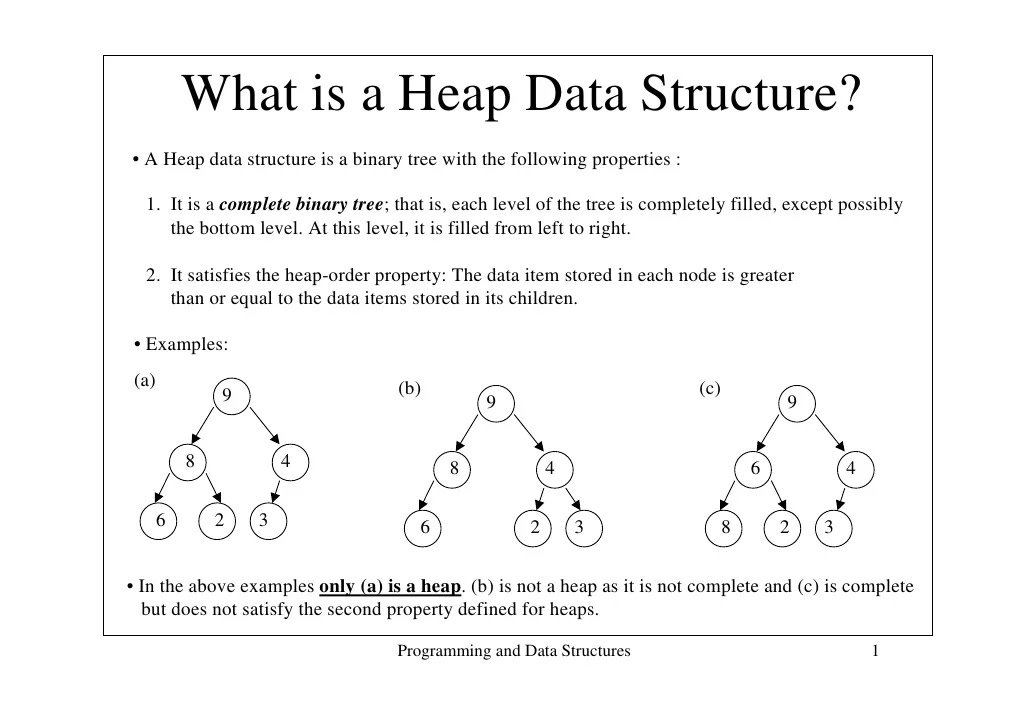
We have also inferred another property about this data structure. An ordered data structure that maintains its ordering, has easy pushing and popping. Sounds an awful like heaps doesn’t it?

We can also have min heaps, where nodes < children. Either way, heaps maintain ordering.

For those of you not too comfortable with Heaps, I will do a breakdown on them soon. For now remember the property that heaps make lots of pushing and popping efficient, when we want to maintain an ordering of data elements.Using heaps will make our code super simple. All we need to do is to do is to heapify our classes based on information gain. Then we pop the maximum value (root node), add the genius, and push it back. Rinse and repeat.

Step 4: Code

Now that we have built everything from scratch, I want you to see how even very complex questions can become very straightforward when done correctly.

import heapq


class Solution:
    def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:
        # priority queue ordered by gain descending
        ratings = [( n / d - (n + 1) / (d + 1),n, d) for n, d in classes]
        heapq.heapify(ratings)

        for _ in range(extraStudents):
            _,m, d = heapq.heappop(ratings)
            r = ((m + 1) / (d + 1) - (m + 2) / (d + 2), m + 1, d + 1)
            heapq.heappush(ratings, r)

        return sum(n / d for _,n, d in ratings) / len(classes)      

You might be wondering why we have flipped the gain calculation. This is because Python only does min heaps. So by taking the negative of the gain (which can be seen as the loss by not adding the genius to the class), we overcome this problem.

That’s it for this. As you can see, by identifying simpler subproblems and refining them, we can create our optimal solutions.

Time Complexity- O(n) to heapify. Then we have to pop k times for O(k log n). Total O(n + k*log n)

Space Complexity- O(n). We are storing the gain/loss to sort things out

Make sure you share your thoughts on this question/any interesting questions/developments in the comments or through my links.

Happy Prep. I’ll see you at your dream job.

Interview Ace,

Devansh <3

Reach out to me on:

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75