[Solution]Problem 41: Create your own Datastructure with O(1) Time complexity (Dropbox)
Data structures, Logic, Object Oriented Programming
Problem
This problem was asked by Dropbox.
Create a data structure that performs all the following operations in O(1) time:
plus: Add a key with value1. If the key already exists, increment its value by one.minus: Decrement the value of a key. If the key's value is currently1, remove it.get_max: Return a key with the highest value.get_min: Return a key with the lowest value.
[FREE SUBS]To buy the solution for this problem, use any of the following links. The price is 3 USD. Once you send the payment, message me on IG, LinkedIn, Twitter, or by Email:
Venmo: https://account.venmo.com/u/FNU-Devansh
Paypal: paypal.me/ISeeThings
Or you can sign up for a Free Trial Below. Thanks to the guaranteed refund policy, there is no risk to you -
Step 1: The Xs and Os
Problems like this are hard for a variety of reasons. Obviously, there will be some challenges in implementing the O(1) time operations. So it makes sense to go for the lower-hanging fruit first. Luckily, the get_min/max functions are easy to reach.
Typically, if we want to return the min/max value, we will track just them using variables. You might be tempted to do so, however that approach has one drawback. Let’s look at the requirements of our DS once more.
plus: Add a key with value 1. If the key already exists, increment its value by one.
minus: Decrement the value of a key. If the key's value is currently 1, remove it.Both these functions tweak our DS in a major way. Notice that for an instance of our DS, there is a chance that our minimum and max values will change if these functions are called a bunch of times on keys. Clearly, we will need to track more than just the max and min value at the current time. For any given key, it thus becomes important to keep track of both the keys with lower and higher counts than it. Fortunately, we have a DS perfectly developed for this bi-directionality.
Step 2: Doubly Linked List
Doubly Linked-Lists are like the big brothers of LinkedLists. They don’t show up as frequently as LLs, but they do have a very important role in software engineering. When we have relationships where bi-directionality is important, you can implement them.
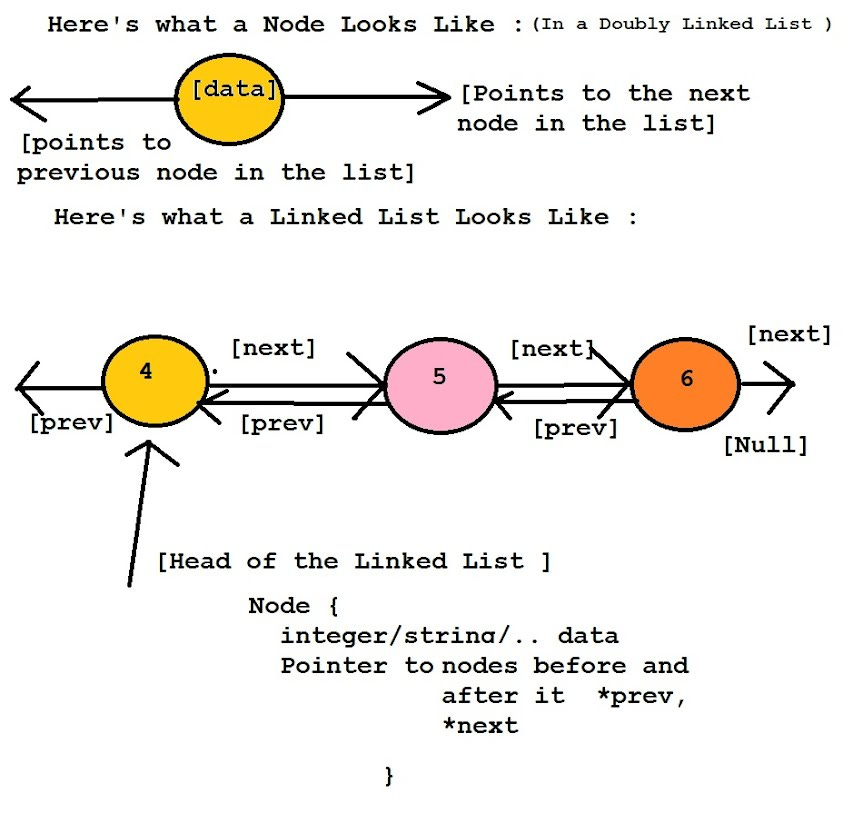
To meet the needs, we would a sorted collection of keys. We store these keys as a doubly-linked list. For a given node, the previous node will contain keys with the next lowest value, and the next node will contain keys with the next highest value. If we maintain a pointer to the head and tail of this list, we will always be able to access a key with the lowest and highest value, respectively in constant time.
Before we start implementing the DLL, we need to develop the Node Class. Most of it is relatively straightforward. Take a look below.
class Node(object):
def __init__(self):
self.key_set = set()
self.prev, self.nxt = None, None
def add_key(self, key):
self.key_set.add(key)
def remove_key(self, key):
self.key_set.remove(key)
def get_any_key(self):
if self.key_set:
result = self.key_set.pop()
self.add_key(result)
return result
else:
return None
def is_empty(self):
return len(self.key_set) == 0
We a set() instead of dict/hash-map because uniqueness matters in our final solution. Remember, each node will track all the keys with the same count. With our node done, let’s create our DLL.
Step 3: Creating The Doubly Linked List
We can code up the doubly linked list class, which will allow us to chain together nodes. The logic of each method here hopefully should not have any surprises. In addition to maintaining head and tail pointers, we define insertion and removal methods that run in O(1) time.
class DoubleLinkedList(object):
def __init__(self):
self.head_node, self.tail_node = Node(), Node()
self.head_node.nxt, self.tail_node.prev = self.tail_node, self.head_node
def insert_after(self, x):
node, temp = Node(), x.nxt
x.nxt, node.prev = node, x
node.nxt, temp.prev = temp, node
return node
def insert_before(self, x):
return self.insert_after(x.prev)
def insert_after_head(self):
return self.insert_after(self.head_node)
def remove(self, x):
prev_node = x.prev
prev_node.nxt, x.nxt.prev = x.nxt, prev_node
def get_head(self):
return self.head_node.nxt
def get_tail(self):
return self.tail_node.prev
The DLL is implemented using the idea of sentinel nodes, i.e. we have two dummy nodes to represent head and tail. Initially head.next points to tail and tail.prev points to head. Using two dummy nodes dramatically simplifies the implementation. We will cover this in Math Mondays soon.
Now that we have finished laying the foundation, it’s time to actually implement the problems that will allow us to create our solution.
Step 4: Sketching up the algorithms
We know that a node in the doubly linked list represents a bucket containing a bag of words with a certain frequency. The DLL is maintained in sorted order with the head node containing words with the least frequency and the tail node containing words with maximum frequency.
The DLL, allows us to implement get_max/min in O(1) by returning any word contained in the tail and head respectively. Next we need 2 dicts to increment or decrement frequency of a key in O(1) and to map the count for every bucket node in the linked list respectively. This is not too hard.
If we can maintain the sorted order of the linked list in O(1) while performing the increment and decrement operations, we would have a working solution. Yippee!!!

So now, let’s figure out the increment/decrement of key counts. Believe it or not, we are very close to fixing everything. We have all the pieces together (mostly). We just have to arrange them properly.
Step 5: Plus/Minus deets
Let’s now implement the final details of this extremely long and tiring question. Let’s quickly work through the steps of this
When we increment a key, we carry out three separate steps:
Increment the corresponding value in our
key counting dictionary(or insert a new key with value1).Add a new key to the corresponding node in
bucket frequency map/DLL. If there is no such node, create a new node to hold this key and insert it at the appropriate position in the linked list.Remove the key from the node that previously stored it.
Decrementing follows a similar process:
Decrement the corresponding value in our
key counting dictionary. If the value is now zero, remove the key.Add a new key to the corresponding node in
bucket frequency map/DLL. If there is no such node, create a new node to hold this key and insert it at the appropriate position in the linked list.Remove the key from the node that previously stored it.
All that’s left to do is code all this up. Let’s get to it.
Step 6: Coding everything
Our final class will look like this-
class AllOne(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.dll, self.key_counter = DoubleLinkedList(), defaultdict(int)
self.node_freq = {}
def _rmv_key_pf_node(self, pf, key):
if pf in self.node_freq:
node = self.node_freq[pf]
node.remove_key(key)
if node.is_empty():
self.dll.remove(node)
self.node_freq.pop(pf)
def inc(self, key):
"""
Inserts a new key <Key> with value 1. Or increments an existing key by 1.
:type key: str
:rtype: void
"""
self.key_counter[key] += 1
cf, pf = self.key_counter[key], self.key_counter[key]-1
if cf not in self.node_freq:
self.node_freq[cf] = self.dll.insert_after_head() if pf == 0 else self.dll.insert_after(self.node_freq[pf])
self.node_freq[cf].add_key(key)
if pf > 0:
self._rmv_key_pf_node(pf, key)
def dec(self, key):
"""
Decrements an existing key by 1. If Key's value is 1, remove it from the data structure.
:type key: str
:rtype: void
"""
if key in self.key_counter:
self.key_counter[key] -= 1
cf, pf = self.key_counter[key], self.key_counter[key]+1
if self.key_counter[key] == 0:
self.key_counter.pop(key)
if cf not in self.node_freq and cf != 0:
self.node_freq[cf] = self.dll.insert_before(self.node_freq[pf])
if cf != 0:
self.node_freq[cf].add_key(key)
self._rmv_key_pf_node(pf, key)
def getMaxKey(self):
"""
Returns one of the keys with maximal value.
:rtype: str
"""
return self.dll.get_tail().get_any_key() if self.dll.get_tail().get_any_key() else ""
def getMinKey(self):
"""
Returns one of the keys with Minimal value.
:rtype: str
"""
return self.dll.get_head().get_any_key() if self.dll.get_tail().get_any_key() else ""This is a lot to take in, so feel free to go save this and go back over it a couple of times. Hopefully, you will see how this solution is about chaining a bunch of smaller problems together.
Time Complexity- O(1)
Space Complexity- O(N) because of the counting dictionaries
Make sure you share your thoughts on this question/solution/any interesting questions/developments in the comments or through my links.
Happy Prep. I’ll see you at your dream job.
Go kill all you Tricky Tactician,
Devansh <3
Reach out to me on:
Instagram: https://www.instagram.com/iseethings404/
Message me on Twitter: https://twitter.com/Machine01776819
My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/
My content:
Read my articles: https://rb.gy/zn1aiu
My YouTube: https://rb.gy/88iwdd
Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75



