[Solution]Problem 5: Generate Random Numbers According to Probability [TripleByte]

Medium Difficulty

Problem

This problem was asked by Triplebyte.

You are given n numbers as well as n probabilities that sum up to 1. Write a function to generate one of the numbers with its corresponding probability.

For example, given the numbers [1, 2, 3, 4] and probabilities [0.1, 0.5, 0.2, 0.2], your function should return 1 10% of the time, 2 50% of the time, and 3 and 4 20% of the time.

You can generate random numbers between 0 and 1 uniformly.

Step 1: Visualizing the Problem

This problem can seem slightly tricky at first. How can you generate random numbers with a fixed probability? How can we use what we’ve been given to solve this problem?

The first hint we’ve been given is that our probabilities will sum to one. This is the same range as the random number generator we are given. Therefore, we can map the probability to domains created by the number generator.

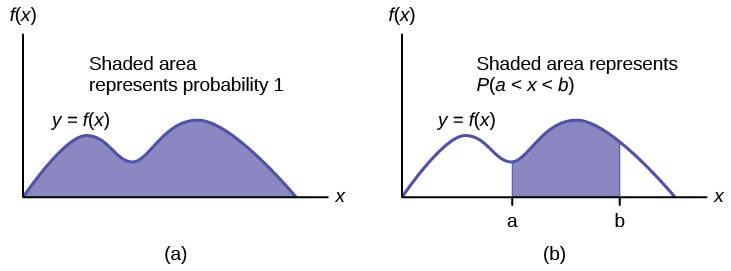
But what mapping should we use? Here is where some knowledge is helpful. One way to visualize probabilities is to take sketch them as areas. Look at the below image for a good visualization.

How does this apply to the question? We could imagine all the probabilities as distinct, disjoint intervals. For example, given the probabilities- [0.1, 0.5, 0.2, 0.2], you would get the intervals [0, 0.1), [0.1, 0.6), [0.6, 0.8), [0.8, 1]. Then we generate uniform random between 0 and 1 and select whichever value corresponding to the interval we fall in. That would look like this:

from random import random

def distribute(nums, probs):
    r = random() #our given 0-1 random number generator

    s = 0
    for num, prob in zip(nums, probs):
        s += prob
        if s >= r:
            return num

This would be an O(n) time and constant space solution? Can we get any better this? Yes and no. Technically speaking, no matter what we do, we will have an O(n) time complexity because we have to traverse the arrays to match our domains to the generated values. And we can’t go any lower than constant space. So what can we do?

Step 2: Optimizing around the context

One interesting thing that the question tells us is that our function might be called multiple times. How do we know this? Remember the wording:

For example, given the numbers [1, 2, 3, 4] and probabilities [0.1, 0.5, 0.2, 0.2], your function should return 1 10% of the time, 2 50% of the time, and 3 and 4 20% of the time.

For a single run, we can’t get any better than our solution in Step 1. But if we work in the fact that we might have multiple calls, then we see a problem. We will recreate identical spaces on every run. This is inefficient. If we can build our list once, and just call our created generator a bunch of times, this would be much better. Since we are building probability ranges, we can build a range once, and binary search over it a bunch of times. In practice, this would like:

from random import random
from bisect import bisect_left

def preprocess(probs):
    lst = []

    current_val = 0
    for p in probs:
        current_val += p
        lst.append(current_val)

    return lst

def distribute(nums, arr):
    r = random()
    i = bisect_left(arr, r)
    return nums[i]

def solution(nums, arr):
    times=int(input("Enter number of random numbers generated"))
    lst=preprocess(arr)
    ma={}
    for _ in range(times):
       rand=distribute(nums,lst)
       if rand not in ma:
           ma[rand]=1
       else:
            ma[rand]+=1
    #   print(rand) 
    print(ma)

solution([1,2,3,4],[0.1,0.5,0.2,0.2])   #testing our solution

And running this code 100,000 times we get:

Which is very close to what we want. This code is O(n) time and space when calling the preprocess, but only logarithmic time when finding the random numbers. Therefore when we have to generate a lot of random numbers, this solution might be preferred.

Note: This is more to show off your ability to consider cases and think beyond the immediate solution, than your typical optimization. It also shows off your knowledge of data structures and algorithms. Solutions like this help you stand out from the crowd, provided you explain why you are doing it.

Closing +Note about the Difficulty Level

Medium questions have a lot of variety. Sometimes they are relatively straightforward, with the challenge coming in the coding. This question, in particular, is difficult because it needs to link to concepts outside coding (probability). Once you realize that the probabilities can be mapped to intervals, the solution becomes pretty easy.

Overall you should be able to solve this question in 35 minutes.

——————————————————————————————————————.

Bonuses/Promotion (Get Free Stuff)

To share interesting problems/solutions with me, reach out to me. Different social media of mine also have other content from me. Good problems and/or solutions receive a free shoutout + 2 months of the paid newsletter:

Reach out to me on Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/