[Solution]Problem 50:Rotting Oranges[Microsoft]

Graphs, BFS, and a lot of love

To learn more about the newsletter, check our detailed About Page + FAQs

To help me understand you better, please fill out this anonymous, 2-min survey

---

I’m sure you got groovy with this problem yesterday,

As I mentioned, this is a question that requires some level of insight and implementation to solve. The concurrent nature of the rotting oranges (multiple oranges rotting at the same time) often overwhelms people if not handled correctly.

How did you do?

This problem can be found as problem 994. Rotting Oranges on Leetcode.

Problem

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,

• 1 representing a fresh orange, or

• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 10

• grid[i][j] is 0, 1, or 2.

You can test your solution here

[FREE SUBS]To buy the solution for this problem, use any of the following links. The price is 3 USD. Once you send the payment, message me on IG, LinkedIn, Twitter, or by Email:

Venmo: https:/ount.venmo.com/u/FNU-Devansh

Paypal: paypal.me/ISeeThings

Or you can sign up for a Free Trial Below. Since the reception has been great, I got a special offer for y’all. You can get this newsletter free for 2 months, just by using the button below-

Step 1: Understanding the setup

While it can be tempting to jump straight into a problem it’s better to take a step back and look over it. This helps you solve everything in a smooth and organized manner, which is crucial to impressing your interviewers. Remember, your interviewers are testing your communication and problem solving as much as they are testing your coding. Well-organized communication allows you to emphasize your strength and knowledge effectively.

Make sure you strengthen all 5 pillars to ace your interviews.

When it comes to this question, we have already noticed one salient feature- the simultaneously rotting oranges. Let’s attack that first to see if we can find any useful hints on how to proceed.

Looking at how the rot spreads through the crate over time, one thing stands out. The oranges rot layer by layer. In the first minute, the oranges immediately next to a rotten orange will go bad. In the next minute, the oranges separated from the originally rotten orange by a single orange will go bad. And so on…

Thus we can come up with the rule-

At time= t minutes
fresh oranges at a distance of t from the closest rotten orange will go bad. 

Here we define the distance between two oranges as the number of connected oranges between the source and the target orange. So if we had a grid [2,0,1] then the distance between the rotting orange and the fresh one would be infinity. Similarly for grid

[[2,0,1], [1,1,1]] the distance between the rotten orange (0,0) and orange at (0,2) would be 3. Take a second to verify that this makes sense to you, and matches the question needs.

It should also be clear that the time it would take for an orange to rot would be

it’s distance from the closest rotting orange + 1 

So far, so good. But what do we do from here?

Step 2: Enter the Graphs

So far the mechanism we’ve described looks an awful lot like BFS. Let’s verify this using the awesome graph techniques I shared with you in this newsletter. First, let’s use our graph spotting framework, discussed on this Math Monday, to verify whether a graph can be useful here. According to that, we are fine if we can decompose our problem into 3 components-

1. Nodes/Entities- These will be the oranges themselves. Both fresh and rotten.

2. Edges/Relationships- Two oranges are related to each other if they are adjacent to each other. This would fit in well with our observations about time/distance earlier.

3. Weighted?- Clearly, there is no difference in any two distinct pairs of adjacent oranges. Thus it makes sense to use an unweighted graph. All oranges rot at identical rates as well. If they made changes, making certain positions harder to reach and/or making some oranges more resistant to rotting, then we would use weighted graphs.

So far, looks like our intuition about this being a graph problem is right on the money. Let’s now confirm whether BFS is the right algorithm. In my Technique Tuesday on finding the correct traversal algorithm, I mentioned that the for shortest path problems, BFS/ its variants are best. Since we are using an unweighted graph, we can simply utilize the BFS algorithm.

Notice we are relying on the distance to rotten oranges to compute the time needed, we would need the shortest distance. Thus we should use the BFS. This aligns perfectly well with our observations.

Using this we can come up with our brute-force solution-

1. From every rotten orange (in the beginning), run a BFS going through all the connected oranges. Rot them as per the rules. For every orange mark the time we took to rot it.

2. If we come across an already rotten orange (from a previous BFS), check the time it took to rot. If it is more than our current time, then update the time (we have found a new closest rotten orange).

3. If we still have fresh oranges at the end of the code, return -1. Otherwise, return the maximum time taken.

How would we know how many fresh oranges there are? And where the rotting oranges are? Simple. We will go through in crate once and mark all these + count the fresh oranges.

However, this approach is terrible. The time complexity of such a solution would be O(o*m*n) where o is the number of rotten oranges in our crate at the start. This is because, in every BFS, we will visit every location in the grid. This is an O(m*n) operation. Since this operation would be repeated o times (for every orange), the overall complexity will become O(o*m*n).

So …how can we improve this?

Here is your hint-

BFS goes level by level. There is no reason we can’t add multiple nodes (gates) to the first level. There’s your hint. Try to work this out for yourself before proceeding

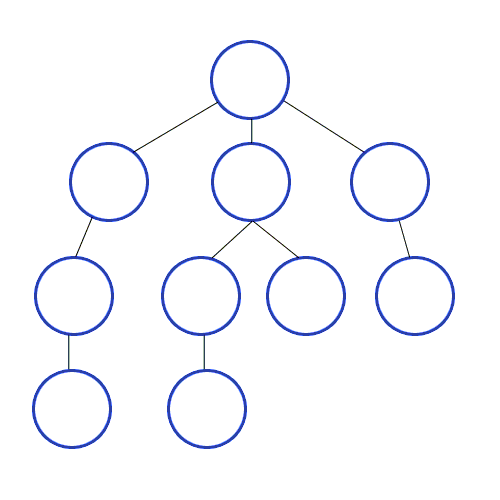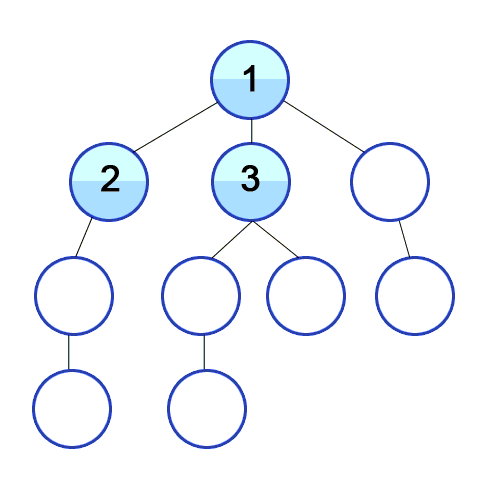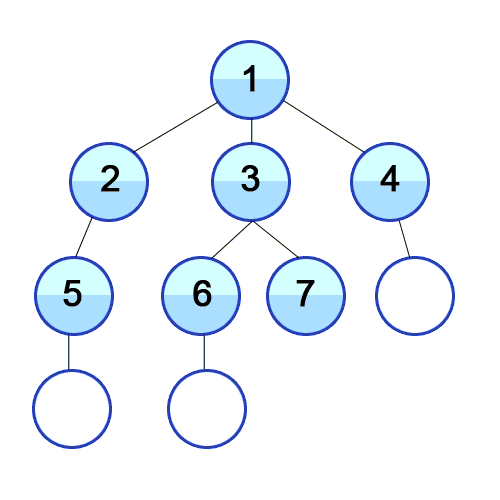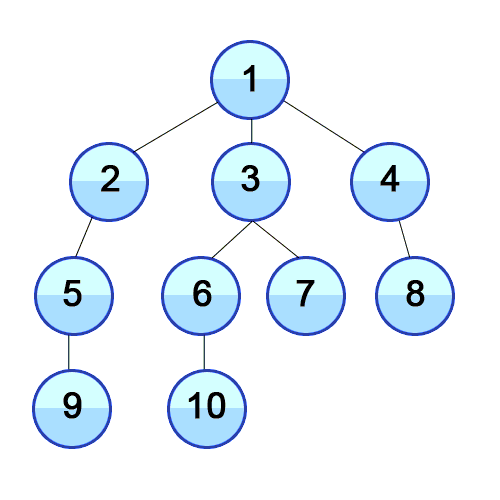
If you’re proceeding, I’m going to assume you tried your best. Remember struggling with the problem is very important to build up all the neural pathways in your mind. So don’t cheat yourself of the gainzzz.

Step 3: Multi-Source BFS

I want you to notice something. For any given fresh orange, there is only one possible rotten orange. If it is equidistant to more than one, we can select any of them.

We can take advantage of the layer-by-layer nature of BFS to put this insight to use. Traditional BFS starts with a single source i.e, a single node at level 1 (distance 0). Let’s look at the logic for BFS for distance mapping

Initialize queue Q
Initialize array d[N] = [INF]*len(Nodes) #for distances from source
Q.enqueue(a)
distance = 0
d[a] = 0
while Q is not empty:
  n = Q.dequeue
  distance = distance + 1
  for each neighbor n_i of n:
    if d[n_i] is infinity:
      d[n_i] = distance
      Q.enqueue(n_i) 

Notice that this will automatically traverse and assign the correct values for distances to one source. If we tweaked the code a little bit to accommodate the starting sources, then we should be to traverse all the distances without major problems.

If this is confusing you, feel to take a breather. Consider your vanilla BFS. Once you have populated your queue with the neighbors of your source, you can basically treat the queue as a list of sources starting on the subgraph. This is because graphs and BFS are inherently recursive. The only difference between the vanilla and a multi-source BFS is that the latter has a populated queue at time/distance 0. This is one of the coolest properties of recursive structures. Even more complex variants of a simple recursive structure can be reduced to your simple structure easily. This is why recursive code is often called elegant. There’s a cool topic to bring up at parties where you’re surrounded by nerds.

We are finally near the end. Let’s put everything together for our solution

Step 4: Coding it all up

Alright, it is time to code everything up. Make sure you have an understanding of all the ideas we discussed till this point. Once you do, the code will be understable.

from collections import deque
class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        rotten_orange = deque()
        minutes = 0
        fresh_orange = 0
        
        rows, cols = len(grid), len(grid[0])
        
        for r in range(rows):
            for c in range(cols):
                orange = grid[r][c]
                if orange == 2:
                    rotten_orange.append((r,c))
                elif orange == 1:
                    fresh_orange += 1
                    
        directions = [(1,0), (-1,0), (0, 1), (0,-1)]
        while rotten_orange and fresh_orange > 0:
            minutes += 1
            
            for _ in range(len(rotten_orange)):
                r, c = rotten_orange.popleft()
                for dr, dc in directions:
                    row = r + dr
                    col = c + dc
                    if row >= 0 and row < rows and col >= 0 and col < cols and grid[row][col] == 1:
                        fresh_orange -= 1
                        grid[row][col] = 2
                        rotten_orange.append((row, col))
                        
        return minutes if fresh_orange == 0 else -1

Time Complexity- O(n*m).

Space Complexity- O(n). Worst case- filled crate + all oranges rotten at the start. Our queue will be filled taking O(n*m) space.

Loved the solution? Hate it? Want to talk to me about your crypto portfolio? Get my predictions on the UCL or MMA PPVs? Want an in-depth analysis of the best chocolate milk brands? Reach out to me by replying to this email, in the comments, or using the links below.

Stay Woke. I’ll see you living the dream.

Go kill all,

Devansh <3

Reach out to me on:

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75