[Solution]Problem 52:Search 2D Matrix[Microsoft]
I'm sure this solution will be quite surprising for a quite a few of you.
To learn more about the newsletter, check our detailed About Page + FAQs
To help me understand you better, please fill out this anonymous, 2-min survey. If you liked this post, make sure you hit the heart icon in this email.
Recommend this publication to Substack over here
Are you ready for this,
Make sure you really understand the solution to this upcoming problem. This problem is special because solving doesn’t really require much special knowledge. Just some logic and the teensiest bit of basic algebra. What makes this problem is not how hard the solution is, but that spotting what to do requires some insight. I love problems like this because they are great for testing your problem-solving skills.
This problem can be found as problem 74. Search a 2D Matrix on Leetcode.
Problem
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.
Example 1:
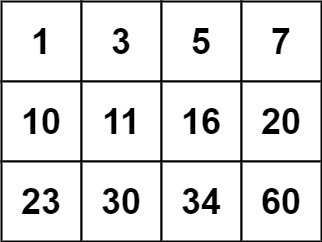
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true
Example 2:
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
You can test your solution here
[FREE SUBS]To buy the solution for this problem, use any of the following links. The price is 3 USD. Once you send the payment, message me on IG, LinkedIn, Twitter, or by Email:
Venmo: httount.venmo.com/u/FNU-Devansh
Paypal: paypal.me/ISeeThings
Or you can sign up for a Free Trial Below. Since the reception has been great, I got a special offer for y’all. You can get this newsletter free for 2 months, just by using the button below-
Step 1: Working on the Brute-Force
Since this problem is pretty straightforward, we can get into the brute-force solution. As we talked about many times in my newsletter, one of the most impactful ways to obtain efficient solutions is to take the brute force solution and cut-down from there.
Our brute force will look relatively simple. We’ll traverse through the matrix, and check through the cells one by one. We’re basically conducting a linear search, on the entire 2D array. The time complexity required would be O(m*n) since we need to check every value. We’d also be using no extra space.
How can we improve this? Obviously, we haven’t really used the properties of the matrix in any way. That would be a good next step. Let’s take a look and see what insights we can come up with.
Step 2: Looking at the matrix rules
We’re given 2 special rules about the matrix-
Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.
Combined, this tells us something interesting- this matrix is sorted in the row-major order. This term might be new to you, but take a look below, and you will see this is typically the order we use when traversing 2D arrays using nested for loops. Make sure you flex this terminology in your interview to gain those sweet brownie points.

Now, most solutions online use this insight and do very little with this. They run binary search twice, once to identify the correct row and another to then get the right column. This isn’t bad, but it’s a really clunky way of doing things. The code you’ll have to run will be much longer than necessary. What I’m going to share with you is much simpler to code up and requires only a little bit more work to come up with. If you will be working with matrices a lot (most professional software devs), then knowing this technique is a must.

Step 3: Shifting between 1D and 2D
Remember how we made this simple observation about the brute force solution- “We’re basically conducting a linear search, on the entire 2D array”? Here is where that simple statement becomes the key to solving this tricky problem. If there is a way to evaluate our 2D array as a sorted 1D array, then we can run our trust pal binary search just once on the whole thing.
We can actually ‘flatten’ 2D matrices into 1D lists and vice-versa. Those familiar with Machine Learning (or anyone very good with matrices) will know this. To those of you that really want to show off your knowledge- know that we can reshape any n-dimensional tensor into any other dimension. What is a tensor you ask? In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. In easier words, think of it as a multidimensional matrix. If a list is a line, a matrix is a square, a tensor can be anything from the line to the square, cube, and beyond.

Just remember to hold very strong eye contact as you talk about tensors. This will raise fear in your interviewers and automatically mark you as the Alpha in the relationship. Bonus points if you ‘bob n weave’ Mike Tyson style while doing this.
Getting back to the question, reshaping the matrix is an expensive operation. But all we need are the indices (to run our search). If we can figure out some rules for identifying what the given location in our 2D matrix would be in our (imaginary) reshaped list, then we can efficiently run our binary search on the whole matrix. Let’s get into that.
Step 4: Figuring out the deets
Let’s work on our rule for switching between indices. To do so, we’ll use a favorite technique in this newsletter, using small test inputs.
Let’s take the matrix [ [1,2,3] [4,5,6]] that follows the rules given to us. We know that to run our binary search solution, we’d need the list [1,2,3,4,5,6]. The index [1][0] would need to become 3 and so on. This transformation would also need to work in reverse- i.e, index 0 becomes [0][0], idx 3 becomes [1][0] and so on. Let’s see if we can work out some basic math equations to match these conditions. Let’s work out the flattening from 2D to 1D first.
It should be clear that the first row will keep their column indices the same. The indices from [0][0] to [0][2] will from to 0-2. The next row will go from 3-5.
More generally, given a matrix of m columns and n rows-
the first row will go from 0 to (m-1),
2nd row- m to (2m-1)
3rd row- 2m to (3m-1)
...
nth row- (n-1)*m to (nm-1)
in the indices if our flattened arrayFeel free to test this to confirm for yourself. What can we do given this information?
Given the location [r][c] in our matrix
Index in 1D array-
r*m+ c = middleIdxLet’s test this. Given [1][0] in our toy array, we return 1*3 + 0= 3. Given [1][2] we get 1*3 + 2=5. Both values check out. Let’s take a bigger example. Consider a 5x5 matrix ranging from with values from 0-24 at the appropriate index.
At start
[0][0]- 0*5 + 0 = 0
[1][0]- 1*5+ 0 = 5
[3][4]- 3*5 + 4= 19
[4][4]- 4*5 + 4= 24So far, so good. Using this we can reverse engineer rules for calculating the row and column index given a middle index in our flattened array-
c=middleIdx-r*m
r= (middleIdx-c)/mSince we’re given the m, the computations are much easier than you would think. c is merely middleIdx%m and r is middleIdx//m (‘//’ stands for integer division. It truncates the floating part, leaving only the int. 3//2 = 1). Take a second to understand why. If you have difficulty with it, you know how to reach me.
Once we’ve figured it out, all our pieces will now fall into place. Time to get into the coding.
Step 5: Coding it up
Our code will do the following things-
Let the beginning index be 0 and end be row*col (which would be the length of our flattened array)
Calculate the middle index using these pointers.
Convert the middle index into the appropriate 2D location using the rule above.
Rest is a standard binary search
Effectively speaking we have turned this into a normal binary search, with a slight modification. This is much easier to work with than the alternative.
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if not matrix:
return False
row = len(matrix)
col = len(matrix[0]) # Number of Columns of the matrix...
beg = 0
end = row*col #treating this as a 1D matrix
while beg < end:
mid = beg + (end - beg) // 2
idx = matrix[mid // col][mid % col];
if idx == target:
return True
if idx < target:
beg = mid + 1
else:
end = mid
return False Time Complexity- O(log(m*n)) = O(log(m)+ log(n))
Space Complexity- O(1)
Loved the solution? Hate it? Want to talk to me about your crypto portfolio? Get my predictions on the UCL or MMA PPVs? Want an in-depth analysis of the best chocolate milk brands? Reach out to me by replying to this email, in the comments, or using the links below.
Stay Woke. I’ll see you living the dream.
Go kill all,
Devansh <3
Reach out to me on:
Instagram: https://www.instagram.com/iseethings404/
Message me on Twitter: https://twitter.com/Machine01776819
My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/
My content:
Read my articles: https://rb.gy/zn1aiu
My YouTube: https://rb.gy/88iwdd
Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75