[Solution]Problem 60:N Queens [FAANG+ everyone else]

Backtracking, Recursion, Chess

Oct 14, 2022

To learn more about the newsletter, check our detailed About Page + FAQs

To help me understand you better, please fill out this anonymous, 2-min survey. If you liked this post, make sure you hit the heart icon in this email.

Recommend this publication to Substack over here

Take the next step by subscribing here

Did you have a good time with this one?

This question has a bit of a reputation in the coding circles because it is one of the hardest ones. After today, you won’t need to be scared of the N-Queens problem anymore.

This problem can be found as problem 51. N-Queens

Problem

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1:

Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1
Output: [["Q"]]

Constraints:

1 <= n <= 9

You can test your solution here

Step 1: Understanding the setup

Unlike many of the hard problems on Leetcode, this question is not hard to understand. This question is not hard because there are a lot of tricks that you have to work through to solve this problem (unlike the 2SAT problem, for example). This problem is tricky because the implementation has a lot of little steps that need to be nailed. But the good news with that is that if we take things step by step, we will arrive at the solution. The secret is to not rush ahead and then get overwhelmed by all the moving details.

For this problem, we largely have the following things we need to do-

Actually, initialize a board and do other setup-related work.
Start placing the queens in the locations

Assuming we have the solution sorted out, 1 is mostly trivial. For 2, it’s not hard to see that we would need to implement backtracking into the solution for this. So let’s start focusing our energy on this.

Step 2: The mechanics of placing our Queens

So how would we go about placing our queens? Usually, when we iterate over a 2D array, we go row by row (in the outer loop). No reason to reinvent the wheel. So we can start from there. Checking if there is a queen occupying a column is not super hard. Just keep track of all cols occupied by a queen.

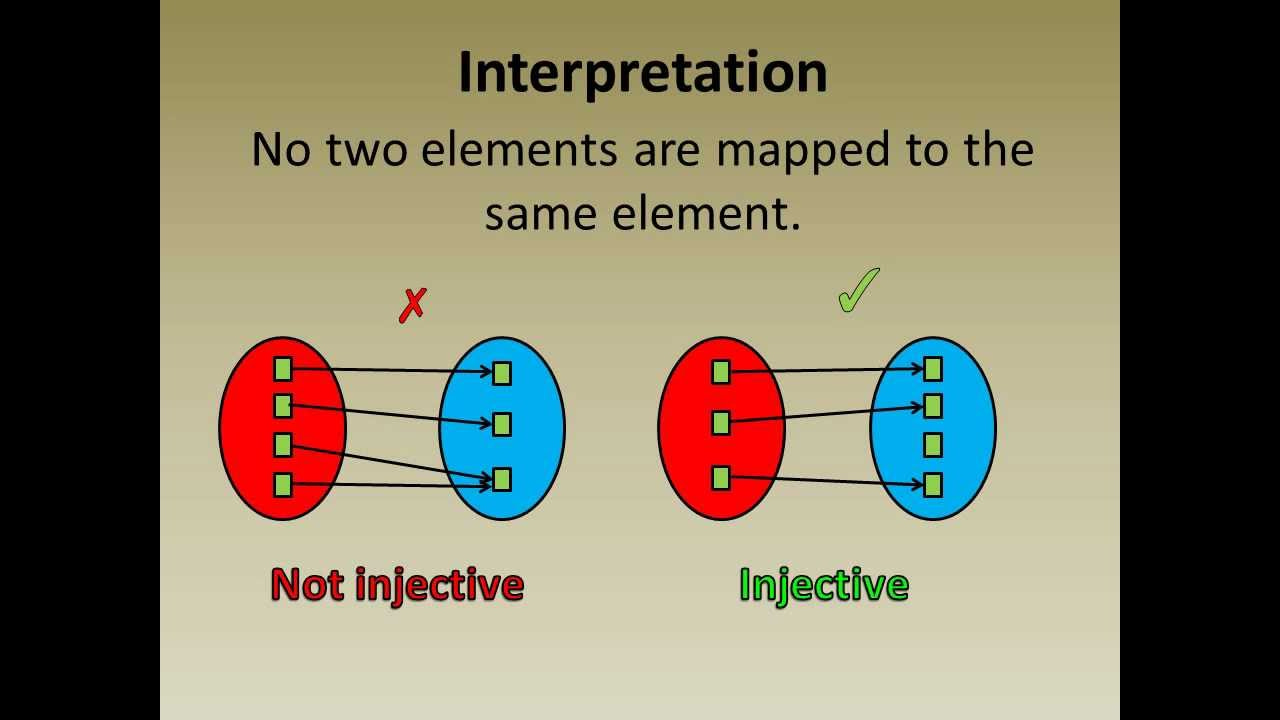
Now here is when we run into our first problem. How do we check for diagonals? We could just traverse through the diagonals, but this would be expensive. Especially we would have to check both kinds of diagonals- the main and the anti. For those of you not familiar with the terms, refer to the image below. For our purposes, we will refer to all the diagonals going from the upper left to lower right as the main diagonals and all the diagonals going from lower left to upper right as anti-diagonals (assuming we read left to right). So [5,1] is a main diag whole [4,5] is an anti-diag.

Are there any patterns about the diagonals that we can figure out? Something that we can check to see if there is a queen on a diag?

Step 3: Diagonal indexing

There is in fact rules for this. For main diagonals the value of (r-c) is constant. For anti-diagonals, r+c will be constant. Furthermore each main diagonal will have a unique difference associated with it(same for the anti-diagonals). Try to figure out why for yourself. It’s good practice for spotting patterns and proving them. If you struggle with it, you can always reach out to me.

For those of that want to get really fancy with it, make sure you use the phrase injective relationship between the difference (or sum) b/w the main diagonal (or anti-diagonal). It means the same thing as the part bolded out, but is a good way to flex your knowledge of discrete math. Make sure you hold strong eye contact with your interviewer, get into a quarter squat, and hit your interviewers with a front double bicep while saying this. This will let know that you’re now in charge.

For your interviews, I would suggest remembering this rule. 2D arrays (matrices) are very common in the interview context, and this is a useful thing to know. You don’t want to spend time deriving the rule. Now back to the solution.

How do we spot whether a diagonal is occupied by a queen? Since we know each diagonal will have a unique value (sum or difference depending on the diagonal), we can just use that to our advantage. Use that value as a key for a hash set. This way we can check if a diag is occupied by a queen.

Excellent. Now we have the means for making sure that our board is in a valid state. This means that we can now get into the backtracking.

Step 4: The Recursive Function

So how would our recursion operate? We know that ultimately, we are recursing over the rows. We want to finish when we are at the nth row. Once we reach this point, we can’t place any more queens.

The other times we want to end would be if we reach an invalid board state. However, in this question, we can actually check for that before we choose to recurse further. This would cut down on computation a bit since we eliminate an extra function call. However, this is not a strict requirement, so if you’re more comfortable checking for invalid states at the start of your functions (it’s how I normally recommend), you should do that. Fluidity is important in the interview, so you should solve things the way that works best for you.

Given a row, we want to check over every column in that row to place our queen. The first valid column we find, we place our queen and keep recursing. The rest is standard backtracking stuff, which we covered here-

Technology Made Simple

The Recursive Function Template[Technique Tuesdays]

To learn more about the newsletter, check our detailed About Page + FAQs To help me understand you better, please fill out this anonymous, 2-min survey. If you liked this post, make sure you hit the heart icon in this email. Recommend this publication to Substack over here…

3 years ago · 3 likes · Devansh

I know I’ve been hammering that template a lot. But that’s only because this is one of the most important aspects to master for your interviews/classes/software engineering. Recursion is one of the most important topics and this template has been a game-changer for many students/readers.

Step 5- Coding it Up

Once we’ve worked out the details, coding the solution is actually not too hard. Once again, I would suggest looking at the code and breaking it down in terms of the template (do that for the other recursion problems we’ve covered here as well). This will help you master the template and solve any recursive problem thrown at you.

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        col = set()
        mainDiag = set()  # (r - c)
        antiDiag = set()  # (r + c)

        res = []
        board = [["."] * n for i in range(n)]

        def backtrack(r):
            if r == n:
                copy = ["".join(row) for row in board]
                res.append(copy)
                return

            for c in range(n):
                if c in col or (r - c) in mainDiag or (r + c) in antiDiag:
                    continue

                col.add(c)
                mainDiag.add(r - c)
                antiDiag.add(r + c)
                board[r][c] = "Q"

                backtrack(r + 1)

                col.remove(c)
                mainDiag.remove(r - c)
                antiDiag.remove(r + c)
                board[r][c] = "."

        backtrack(0)
        return res

Time Complexity- O(N!). We have to check for every possible board permutation.

Space Complexity- O(N). We have to track queens in diagonals and cols.

Loved the solution? Hate it? Want to talk to me about your crypto portfolio? Get my predictions on the UCL or MMA PPVs? Want an in-depth analysis of the best chocolate milk brands? Reach out to me by replying to this email, in the comments, or using the links below.