[Solution]Problem 72: Permutation in String [Amazon]
Binary Search Trees, Recursion, Graph Traversal Algorithms
If you like my writing, I would really appreciate an anonymous testimonial. You can drop it here.
To learn more about the newsletter, check our detailed About Page + FAQs
To help me understand you better, please fill out this anonymous, 2-min survey. If you liked this post, make sure you hit the heart icon in this email.
Recommend this publication to Substack over here
Take the next step by subscribing here
How did you with this question? I’d love to hear from you.
This problem can be found as problem 98. Validate Binary Search Tree
Problem
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.
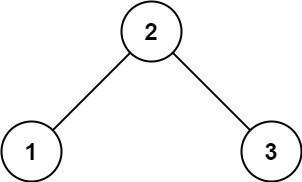
Example 1:
Input: root = [2,1,3]
Output: true
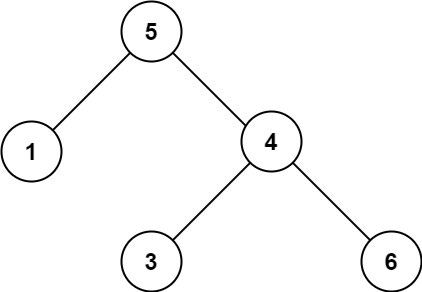
Example 2:
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.
Constraints:
The number of nodes in the tree is in the range
[1, 104].-2^31 <= Node.val <= 2^31 - 1
You can test your solution here
Step 1: Going through the Brute Force
This is a relatively straightforward question to understand. BST are ideas that you should all be familiar with(If you’re struggling with them, make sure you check out the how Master DSA guide here). Since they are such a core concept, I don’t think any interviewer would need you to flesh out the nuances and really look into the definitions. Therefore it makes a lot more sense to jump into creating the brute-force first, since it saves you a lot of time.
What would the brute force of this validation be. Simple. We could do the following-
start at the node.
Check if children are compliant with the requirement
Then keep going down, checking if the other descendants match meet this requirement. This should make a few things clear. The brute-force would implement a kind of recursive DFS. We would use a node and we go through every subtree to confirm whether the subtree is a BST, both by itself, and with the original source node.
This solution would work. But as with all brute-force solutions, it will be slow. Pause right here and try to calculate the time complexity of this approach. If you get it right, you get ice-cream.
No cheating.
Trust me, this is good practice.
Running this operation will require O(N^2) time complexity. For every node, you have to check both the children, and all it’s the other descendants in the subtree. This goes out of control since you have to do this for every node in the tree.
So how do we improve this? We go back to our reliable way of optimizing the solution from the brute-force. We analyze the brute-force, and identify what properties about the inputs we are not utilizing. Once we understand this, we can look for solutions by optimizing the slow portions.
Prepare to get jiggy.
Step 2: Looking at the Brute Force
So what makes our brute force solution…brutish?
The major operation we perform is the comparison. In our current approach, we’re doing a lot of repeated work. Once we already validate a parent subtree, we know that the children trees are valid. However, out current approach doesn’t allow that. It will then cover the children tree as well. And on and on and on….
One way to get around this remember a very basic rule in math. If A>B and B>C, then A>C. Same for the lesser than relation. To those of you that want to really flex your knowledge in interviews, this is called the transitive property. Make sure you hit the interviewer with the sweetest Johnny Bravo pose as you spit these words out. Adds a lot of extra impact.
Why is this relevant? Look back our current brute-force. We do a lot of repeated work because once we have validated one subtree, we don’t discard all of our computations to get the results. We don’t really take advantage of the unique structure of the Binary Search Tree or the transitive property of inequality to speed up our operations. So as a natural next step, it’s now time to look into this.
Step 3: Improving Our Solution
Let’s take a second to think about what truly makes a valid BST. Given a node can we come up with some rules to determine if it is part of a valid subtree?
We know that a node has to be greater than all the nodes to it’s left and smaller than all the nodes to it’s right. Another, easier way to say this is that it must be in a certain range. It will have to be greater than the biggest value to it’s left and lesser than the smallest value to it’s right.
We encode this insight with the following condition-
(node.val < right and node.val > left)So how do we go about getting the left and right?
We already know what they are. We will get them from the nodes we have already visited. How? Here is the process-
We know that if we consider just the root, then every value is a valid BST. Thus, our left and right range would be bounded between +/- infinity.
If we go to the left subtree of a node, then we know that the node’s value is the maximum acceptable value. Anymore, and our tree is no longer to a BST. Thus we should step into the subtree and change the right bound to the node.val.
The opposite is true when we step into the right subtree. Now, every value must be greater than the current node value. So we change the left bound to reflect this property.
This gives us all the necessary pieces to put the final solution. Before you proceed, drink some water. Reread everything we have covered so far. Make sure it makes sense. Step away from the screen and come back in 10 minutes. Make sure things still make sense. This is a very problem-solving heavy question. Making sure you understand the flow of ideas is crucial. If you don’t understand anything after re-reading, leave it in the comments, message me using my social media links, or simply reply to this email. It’s extremely important you understand the details.
Now let’s get to coding things up.
Step 4: Coding It Up
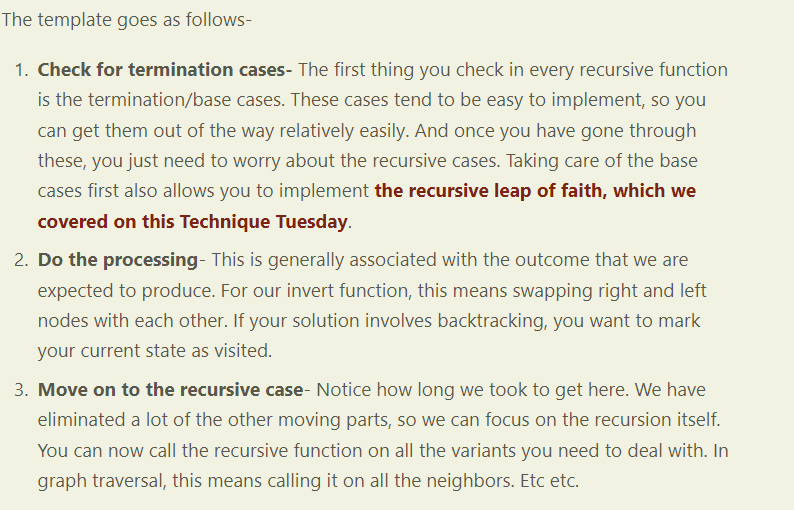
If you’re here, coding things should not be too hard. If you have a hard time coming up with code in a methodical way, check out the recursive template that we covered here. Since we don’t have any side effects, the first 3 steps are the ones that are relevant. Take a look at the them below-
Now compare this with the solution code. Notice how smoothly this works. I wrote this template months ago. That is the power of drilling down to the basics and building up from there.
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
def valid(node, left, right):
if not node:
return True
if not (node.val < right and node.val > left):
return False
return valid(node.left, left, node.val) and valid(node.right, node.val, right)
#call the helper
return valid(root, float('-inf'), float('inf'))
Time Complexity- O(n)
Space Complexity- O(log n) [counting the stack frame]. Worst case O(n)- happens when tree is very unbalanced.
Loved the solution? Hate it? Want to talk to me about your crypto portfolio? Get my predictions on the UCL or MMA PPVs? Want an in-depth analysis of the best chocolate milk brands? Reach out to me by replying to this email, in the comments, or using the links below.
Stay Woke,
Go kill all,
Devansh <3
Reach out to me on:
Instagram: https://www.instagram.com/iseethings404/
Message me on Twitter: https://twitter.com/Machine01776819
My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/
My content:
Read my articles: https://rb.gy/zn1aiu
My YouTube: https://rb.gy/88iwdd