A pragmatic introduction to Fractals [Math Mondays]

The OG AI Art: Fractals are a lot more useful than you would think

Apr 09, 2024

Hey, it’s your favorite cult leader here 🐱‍👤

Mondays are dedicated to theoretical concepts. We’ll cover ideas in Computer Science💻💻, math, software engineering, and much more. Use these days to strengthen your grip on the fundamentals and 10x your skills 🚀🚀.

To get access to all the articles and support my crippling chocolate milk addiction, consider subscribing if you haven’t already!

Help me buy chocolate milk

p.s. you can learn more about the paid plan here.

Recently, we did an extensive deep-dive into Chaotic Systems and how we can use AI to model them better. As we pointed out there, Fractals were a recurring theme in many models for chaotic systems. So I figured it would make sense to do a deeper look into Fractals. As you will see in this article, Fractals have 3 properties that make them immensely appealing to any engineer and researcher:

They show up in a lot of places: Fractals have a very interesting tendency to show up in places where you don’t expect them. We will cover some diverse use cases/fields where we can spot fractals.
Their Math is Super Special: Fractals are created by dancing at the edge of order and chaos. And I’m not being poetic here (this is literally how we create fractals). That gives them some very interesting properties that we don’t see with a lot of other systems that we study.
They are Beautiful: There is an aesthetic to Fractals that you would not find anywhere else. It can be a lot of fun playing around with different functions to create the coolest fractal. Too many people never engage deeply with higher-level math b/c schools are horrible at teaching the introductory stuff, but such hands-on experiences can be great for sparking the curiosity to look deeper.

Let’s look into these points in more detail.

Practical Applications of Fractals

Biomedical Engineering

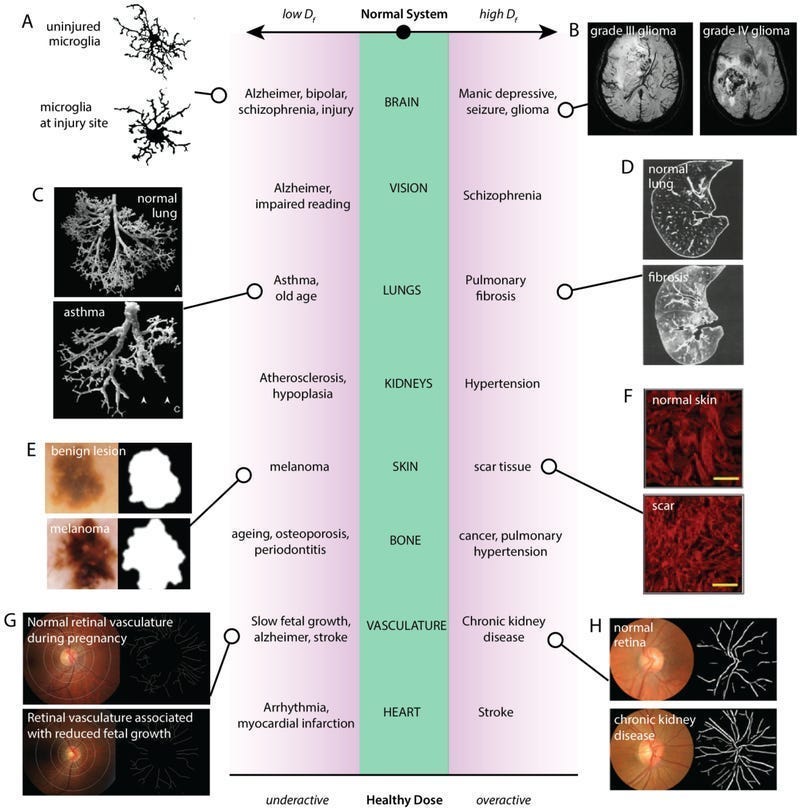
Turns out that Fractals exist in our bodies. And their existence can be crucial for better health. Having too little or too much fractalness in our organs can be a direct quantification of ill health. Think about that for a second.

Optimal levels of chaos and fractality are distinctly associated with physiological health and function in natural systems. Chaos is a type of nonlinear dynamics that tends to exhibit seemingly random structures, whereas fractality is a measure of the extent of organization underlying such structures. Growing bodies of work are demonstrating both the importance of chaotic dynamics for proper function of natural systems, as well as the suitability of fractal mathematics for characterizing these systems. Here, we review how measures of fractality that quantify the dose of chaos may reflect the state of health across various biological systems, including: brain, skeletal muscle, eyes and vision, lungs, kidneys, tumours, cell regulation, wound repair, bone, vasculature, and the heart. We compare how reports of either too little or too much chaos and fractal complexity can be damaging to normal biological function… Overall, we promote the effectiveness of fractals in characterizing natural systems, and suggest moving towards using fractal frameworks as a basis for the research and development of better tools for the future of biomedical engineering.
-A Healthy Dose of Chaos: Using fractal frameworks for engineering higher-fidelity biomedical systems

For a more visual example, take a look at the following image. You can see how the different organs all have fractal-like structures, and how too little or too much fractalness causes serious problems.

“Although the basis for fractal behaviour in natural systems is still unclear, its relationship to physiological state is much more pronounced. Variability has been analyzed with chaos and fractal theory in many different physiological systems, and the measure of fractality has been demonstrated to be associated with the state of health of the system”.

Natural Pattern Simulation: Fractals are excellent at modeling natural phenomena like coastlines, mountain ranges, clouds, and even the distribution of galaxies. Without fractals, natural shapes are difficult to describe precisely using traditional geometrical objects (lines, circles, spheres). Fractals offer us a new mathematical language to accurately model the complexity of our world.

The pervasiveness of Fractal patterns in nature hints at underlying principles of organization in creation. If we can figure out the underlying processes that govern growth and formation in the various fractal-entities our ability to make model the world and make predictions about it would skyrocket. The ability to model natural phenomena with fractals holds the potential for improved understanding and even prediction in fields like meteorology (clouds), geology (mountains), and cosmology (galaxy distribution).

Compression:

There is a class of algorithms that utilize fractals for compressing images. This works fairly well for images with natural textures.

Fractal image compression works on the assumption that many real-world images have self-similar patterns within them. Take my beautiful, flawless skin. Most of my skin looks mostly like other parts of my skin (especially on the same body part). In nerd-talk: my skin is mostly self-similar. Fractal algorithms search for these self-similar sections within the image and store them as mathematical formulas or transformations.

Fractal compression can achieve incredibly high compression ratios. While there is some loss of image quality (hence, lossy compression), the results can be surprisingly good, especially for images with natural textures. Fractal compression also features resolution independence — the decompressed image can be scaled to larger sizes without as much of the blocky pixelation seen in traditional methods. However, the encoding process is slow, and the method isn’t suitable for every image type.

Recently, I learned that this might also be true in human language-

We establish that language is: (1) self-similar, exhibiting complexities at all levels of granularity, with no particular characteristic context length, and (2) long-range dependent (LRD), with a Hurst parameter of approximately H=0.70. Based on these findings, we argue that short-term patterns/dependencies in language, such as in paragraphs, mirror the patterns/dependencies over larger scopes, like entire documents. This may shed some light on how next-token prediction can lead to a comprehension of the structure of text at multiple levels of granularity, from words and clauses to broader contexts and intents. We also demonstrate that fractal parameters improve upon perplexity-based bits-per-byte (BPB) in predicting downstream performance.
-Fractal Patterns May Unravel the Intelligence in Next-Token Prediction

Compressing Language by using Fractals might be the next frontier of Language Model Compression (there is a lot of redundancy baked into LLMs owing to their scale). This is where the self-similarity of Fractals might play a very interesting role.

Figure 1. Manifestations of processes across different time scales. A region marked in red corresponds to the magnified plot above it. TOP: The process exhibits self-similarity with rich details at all levels of granularity. It is an integral process (Xt)t∈N calculated from Wikipedia (see Section 2). BOTTOM: Example of a process that is not self-similar, looking smoother at larger time scales

AI Models

Take a look at this image-

The way I see it, if we can come up with models/functions that encode when neural networks will converge or diverge: we will be able to significantly speed up the entire AI Training process. This is still very much in the research stage for me, and I’ll be posting updates as I learn them. Keep your eyes peeled there.

The Math Behind Fractal Generation

So how are fractals generated? At their core, many fractals are generated using iterations of simple mathematical formulas. This iterative process is where the self-similar nature of fractals arises.

Consider one of the most famous fractals, the Mandelbrot set. Here’s the fundamental formula:

z(n+1) = z(n)^2 + c

z and c are complex numbers.
We start with z(0) = 0.
We recursively compute a new value based on the formula above.

There are two possible outcomes, based on your choice of z and c. The function can either diverge to infinity or remain happily bounded depending on our choice. Fractals are often defined by the boundary between hyperparameters where function iteration diverges or remains bounded. Hence the dancing on the edge of order and chaos.

Try playing around with the function and see how the function produces different outputs.

Generating Fractals

It would be criminal of me to write an article on Fractals and not take a crack at generating them myself. Here is what I’ve been able to do so far (code shared after that images).

If you want, here is the code used to generate the images. Please feel free to play around with it, and improve it however you can. I’d love to see what kinds of changes you make. Come drop your changes on the Github over here.

If you’re looking for some interesting side-projects, building something fractal-related might be. If you do make something special, make sure you tag me/DM me so that I can share it with our cult.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 1. Koch Snowflake
def koch_snowflake(n):
    if n == 0:
        return [[0, 0], [1, 0]]
    else:
        prev_lines = koch_snowflake(n-1)
        new_lines = []
        for p1, p2 in zip(prev_lines[:-1], prev_lines[1:]):
            p1 = np.array(p1)
            p2 = np.array(p2)
            new_lines.append(p1)
            new_lines.append(p1 + (p2 - p1) / 3)
            new_lines.append((p1 + p2) / 2 + np.array([-(p2 - p1)[1], (p2 - p1)[0]]) / 3)
            new_lines.append(p1 + 2 * (p2 - p1) / 3)
        new_lines.append(prev_lines[-1])
        return new_lines

# 2. Sierpinski Triangle
def sierpinski(n):
    if n == 0:
        return [[0, 0], [1, 0], [0.5, np.sqrt(3)/2]]
    else:
        prev_tri = sierpinski(n-1)
        new_tri = []
        for vertex in prev_tri:
            new_tri.append(vertex)
            new_tri.append([vertex[0] + 1, vertex[1]])
            new_tri.append([vertex[0] + 0.5, vertex[1] + np.sqrt(3)/2])
        return new_tri



# 4. Barnsley Fern (Barnsley's Fern)
def barnsley_fern(n):
    x, y = 0, 0
    points = [[x, y]]
    for _ in range(n):
        r = np.random.rand()
        if r <= 0.01:
            x, y = 0, 0.16 * y
        elif r <= 0.86:
            x, y = 0.85 * x + 0.04 * y, -0.04 * x + 0.85 * y + 1.6
        elif r <= 0.93:
            x, y = 0.20 * x - 0.26 * y, 0.23 * x + 0.22 * y + 1.6
        else:
            x, y = -0.15 * x + 0.28 * y, 0.26 * x + 0.24 * y + 0.44
        points.append([x, y])
    return points

# 5. Lorenz Attractor
def lorenz_attractor(sigma=10, rho=28, beta=8/3, dt=0.01, num_steps=10000):
    x, y, z = 0, 1, 1.05
    points = [[x, y, z]]
    for _ in range(num_steps):
        dx = sigma * (y - x) * dt
        dy = (x * (rho - z) - y) * dt
        dz = (x * y - beta * z) * dt
        x, y, z = x + dx, y + dy, z + dz
        points.append([x, y, z])
    return points

# 6. Menger Sponge (3D fractal)
def menger_sponge(n):
    if n == 0:
        return [[0, 0, 0], [1, 0, 0], [1, 1, 0], [0, 1, 0],
                [0, 0, 1], [1, 0, 1], [1, 1, 1], [0, 1, 1]]
    else:
        prev_sponge = menger_sponge(n-1)
        new_sponge = []
        for p1, p2 in zip(prev_sponge[:-1], prev_sponge[1:]):
            new_sponge.extend([p1, p2])
            if np.linalg.norm(np.array(p1) - np.array(p2)) > 1:
                for i in range(1, 3):
                    new_sponge.append([(p1[0] * i + p2[0] * (3 - i)) / 3,
                                       (p1[1] * i + p2[1] * (3 - i)) / 3,
                                       (p1[2] * i + p2[2] * (3 - i)) / 3])
        return new_sponge



# 9. Mandelbrot Set
def mandelbrot(c, max_iter=100):
    z = 0
    n = 0
    while abs(z) <= 2 and n < max_iter:
        z = z*z + c
        n += 1
    return n

def mandelbrot_fractal(width, height, zoom=1, x_off=0, y_off=0, max_iter=100):
    img = np.zeros((width, height))
    for x in range(width):
        for y in range(height):
            zx = 1.5 * (x - width / 2) / (0.5 * zoom * width) + x_off
            zy = (y - height / 2) / (0.5 * zoom * height) + y_off
            c = complex(zx, zy)
            img[x, y] = mandelbrot(c, max_iter)
    return img

# 10. Mandelbulb
def mandelbulb(x, y, z, max_iter=100):
    c = complex(x, y)
    z = complex(0, z)
    n = 0
    while abs(z) <= 2 and n < max_iter:
        z = z**8 + c
        n += 1
    return n

def mandelbulb_fractal(size, max_iter=100):
    x = np.linspace(-2, 2, size)
    y = np.linspace(-2, 2, size)
    z = np.linspace(-2, 2, size)
    fractal = np.zeros((size, size, size))
    for i in range(size):
        for j in range(size):
            for k in range(size):
                fractal[i, j, k] = mandelbulb(x[i], y[j], z[k], max_iter)
    return fractal

# Generate and plot each fractal
plt.figure(figsize=(15, 20))

# 1. Koch Snowflake
plt.subplot(5, 2, 1)
koch_points = koch_snowflake(4)
koch_xs, koch_ys = zip(*koch_points)
plt.plot(koch_xs, koch_ys, 'k')
plt.fill(koch_xs, koch_ys, 'k', alpha=0.3)
plt.title("Koch Snowflake")

# 2. Sierpinski Triangle
plt.subplot(5, 2, 2)
sierpinski_points = sierpinski(4)
sierpinski_xs, sierpinski_ys = zip(*sierpinski_points)
plt.plot(sierpinski_xs, sierpinski_ys, 'k')
plt.fill(sierpinski_xs, sierpinski_ys, 'k', alpha=0.3)
plt.title("Sierpinski Triangle")


# 4. Barnsley Fern
plt.subplot(5, 2, 3)
barnsley_points = barnsley_fern(10000)
barnsley_xs, barnsley_ys = zip(*barnsley_points)
plt.scatter(barnsley_xs, barnsley_ys, s=0.1, color='green')
plt.title("Barnsley Fern")

# 5. Lorenz Attractor
plt.subplot(5, 2, 4, projection='3d')
lorenz_points = np.array(lorenz_attractor())
plt.plot(lorenz_points[:,0], lorenz_points[:,1], lorenz_points[:,2], color='blue')
plt.title("Lorenz Attractor")

# 6. Menger Sponge (3D fractal)
ax = plt.subplot(5, 2, 5, projection='3d')
menger_points = np.array(menger_sponge(3))
ax.scatter(menger_points[:,0], menger_points[:,1], menger_points[:,2], color='orange')
ax.set_title("Menger Sponge")


# 9. Mandelbrot Set
plt.subplot(5, 2, 6)
mandelbrot_img = mandelbrot_fractal(300, 300, zoom=1, max_iter=100)
plt.imshow(mandelbrot_img.T, cmap='inferno', extent=[-2, 1, -1.5, 1.5])
plt.title("Mandelbrot Set")

# 10. Mandelbulb
plt.subplot(5, 2, 7)
mandelbulb_img = mandelbulb_fractal(20, max_iter=100)
plt.imshow(np.max(mandelbulb_img, axis=2), cmap='inferno', extent=[-2, 2, -2, 2])
plt.title("Mandelbulb")

plt.tight_layout()
plt.show()

That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. If you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow.

Save the time, energy, and money you would burn by going through all those videos, courses, products, and ‘coaches’ and easily find all your needs met in one place at ‘Tech Made Simple’! Stay ahead of the curve in AI, software engineering, and the tech industry with expert insights, tips, and resources. 20% off for new subscribers by clicking this link. Subscribe now and simplify your tech journey!

Using this discount will drop the prices-

800 INR (10 USD) → 640 INR (8 USD) per Month

8000 INR (100 USD) → 6400INR (80 USD) per year (533 INR /month)

Get 20% off for 1 year