[Solution]Problem 61:Increasing Order Search Tree [Apple]

Trees, Recursion, Data Structure, Traversal

To learn more about the newsletter, check our detailed About Page + FAQs

To help me understand you better, please fill out this anonymous, 2-min survey. If you liked this post, make sure you hit the heart icon in this email.

Recommend this publication to Substack over here

Take the next step by subscribing here

---

Let’s get right into this

This problem can be found as problem 897. Increasing Order Search Tree

For my Python people, there is a way to do this using ‘yield’ which might give slightly better performance, but that is a language-specific trick, so my solution is not going to cover that. It’s not important enough to make a meaningful difference in your interviews.

Problem

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

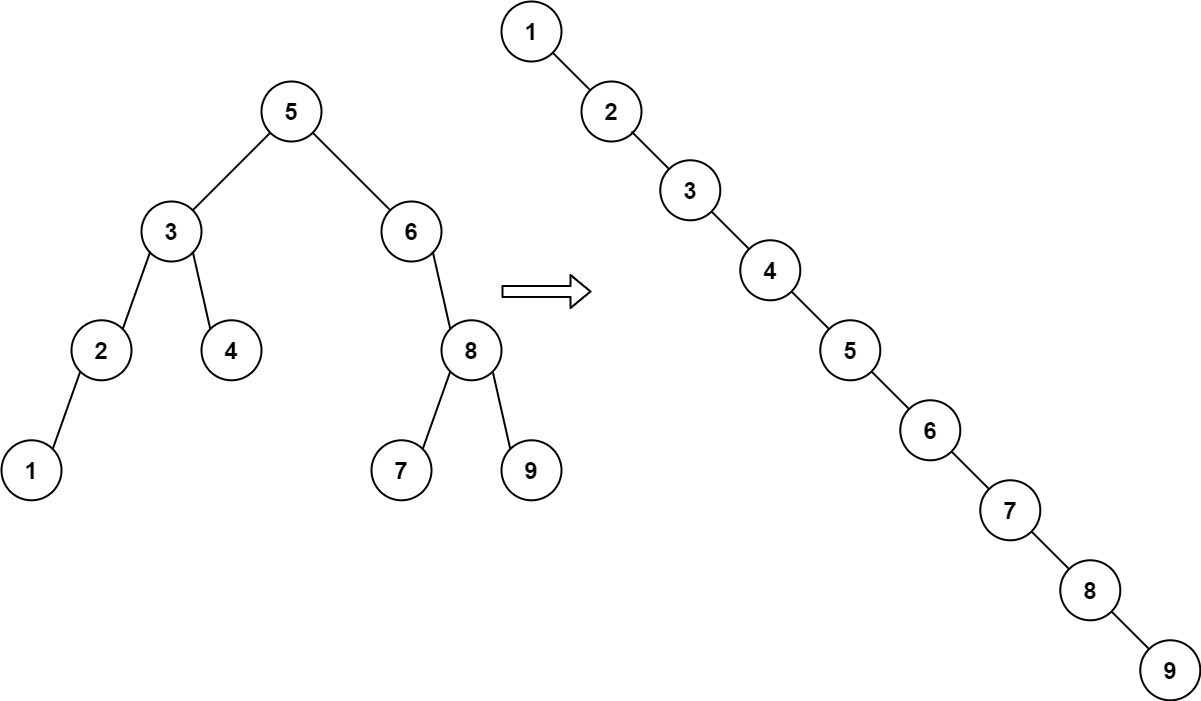
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

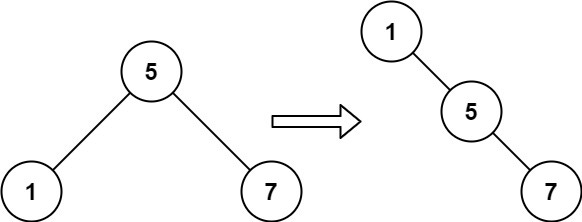
Input: root = [5,1,7]
Output: [1,null,5,null,7]

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].

• 0 <= Node.val <= 1000

You can test your solution here

Step 1: Understanding the Question

As with most other questions, we will first understand what this question is asking. Understanding it can help us create the optimal solution in an efficient manner. Remember your interviews are as much about optics as they are about coding. If you solve the question in a neat and fluid way, your interviewer will give you a much stronger hiring decision. If you stutter around (or solve it without saying anything), your chances go wayyy down.

We can clearly see what we’re expected to do. Convert the Binary Search Tree into a sorted list-like tree. Let’s start fleshing out some more details to see what we can do to figure out the solution.

Clearly, the ordering matters a lot. Specifically, we want to order the tree by node values in ascending values. Fortunately, there are tree traversal algorithms for different situations. Is there any that will fit this situation?

Step 2: In-Order Traversal

Remember, the question gives us a Binary Search Tree. This is a binary tree with a special property-

left child val <= parent val <= right child val 

If we want to print the values in ascending order, we can leverage the in-order traversal. You should know this algorithm because it is one of the most basic concepts of trees. If you want me to do an overview of it (or other traversals), reply to this email and let me know. You can also use any of my social media links to reach out if you prefer that. Lastly, if none of these options work- just say my name 3 times standing in front of a mirror with a glass of chocolate milk. If you say it with a lot of love, I will appear in front of you.

To those of you that need a refresher on in-order traversal, look at the gif below.

Image Source

We can use this to create our naive solution. Simply traverse the tree in-oder, and store all the nodes into a list. Then create a binary tree from this list. This will not take a long time to code up, and will actually be the same time complexity as our optimal solution (both O(N)). Keep in mind, we can’t below this bound since we have to hit every node at least once.

To those of you looking to improve your coding, code this up. It’ll be good practice. In your interviews, you should avoid coding the naive solution (to save time), but right now it will sharpen your skills. If you are more intermediate/advanced, you can skip coding the naive solution.

So how can we optimize this? Let’s start thinking of ways we can reduce the overall time and space usage. The latter has a clear direction- replace the list with a node. This is more efficient memory-wise since we don’t have to store an extra list when converting it into our tree. But to do so, we need to come up with an algorithm for switching our nodes out efficiently. Let’s come up with that.

Step 3: Looking for a pattern

Let’s start looking for a pattern. How do we do that?

We know that we still need to go in order. That part hasn’t changed. So logically, what changes is the code we write for when we do hit our node. If you’re new here, notice how quickly we have narrowed down the scope of what we have to do. Coding Interviews and Leetcode style problems can be overwhelming because they have multiple moving parts. By picking one thread at a time, you can unknot them.

For our solution, we will need to track 2 nodes, the current parent (in our new list) and the current root of the tree or sub-tree. We’ll use cur and node to refer to them respectively.

So what should we do when we do hit a node? We know that the node will not have a left (look at the outputs). So we can immediately say that

node.left = null

Here is where it gets interesting. Remember that in-order traversal is coded as the following-

#assume we take care of base case
inoder(node.left)
#processing step
node.val #do whatever with this value
inorder(node.right)

This means that when we hit the processing step, we have already traversed through the all left nodes. Since we have a BST, we know that the current node is the lowest in the remaining nodes. So what do we want to do?

In our final result, we want our smaller nodes to be the parent. In a small BST (3,1,4), we want 1 being the parent for 3, which would be the child for 4. So let’s work through this.

We will first hit 1. We want to set its left child to null and 1 is our current node. The right child of 1 would be all the remaining values (since we know they are bigger). This means that our cur now becomes the root of our sub-tree, and then hit the recursion for the right.

This might be a little weird to read, so take a look at the code for it-

if node:
                inorder(node.left)
                node.left = None #we have already dealt with left
                cur.right = node
                cur = node # now we want to work on the next node
                inorder(node.right)

This might seem a little strange so I would suggest working through a few small trees to get the pattern. It’s hard to explain this particular part since there isn’t a trick or technique to getting this. Just some trial and error with a few test cases. The best way to learn from this is to work through a few small trees by hand and see if the pattern you find matches this.

Step 4: Coding It Up

If you can work out the pattern, coding it up will not be too difficult. Especially if you went through the recursive function template, which I covered here. Take a look at the code-

class Solution(object):
    global cur # we want this accessible everywhere
    cur= TreeNode(None)
    def increasingBST(self, root):
        def inorder(node):
            global cur
            if node:
                inorder(node.left)
                node.left = None #we have already dealt with left
                cur.right = node
                cur = node
                inorder(node.right)

        ans  = cur 
        inorder(root)
        return ans.right #remember our ans's first val is a None (declaration)

Once again, this isn’t the neatest problem. Especially if you aren’t familiar with trees. However, it is important to solve such problems occasionally. If you had a hard time with this question, then I would suggest solving some of the other tree questions I have solved. You can find them by heading to the archives of my substack, right here

Time Complexity- O(N).

Space Complexity- O(N)

Loved the solution? Hate it? Want to talk to me about your crypto portfolio? Get my predictions on the UCL or MMA PPVs? Want an in-depth analysis of the best chocolate milk brands? Reach out to me by replying to this email, in the comments, or using the links below.

Stay Woke. I’ll see you living the dream.

Go kill all,

Devansh <3

Reach out to me on:

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75