[Solution]Problem 69: Generate Random Numbers According to Probability [TripleByte]

Logic, Problem Solving, Math

To learn more about the newsletter, check our detailed About Page + FAQs

To help me understand you better, please fill out this anonymous, 2-min survey. If you liked this post, make sure you hit the heart icon in this email.

Get a free Weekly Summary of the important updates in AI and Machine Learning here

Recommend this publication to Substack over here

Take the next step by subscribing here

---

How did you do yesterday?

The optimization for this is very different from traditional Leetcode problems. That’s why I love this problem. It requires you to think like a software engineer and consider the life cycle of your solution. I also love that this solution is not gimmicky. Any coder with problem-solving ability, coding skills, and some insight will be able to solve this. You don’t need to know some complex data-structure or memorize an esoteric algorithm for this. The solution is a pure demonstration of your competence in problem-solving.

Problem

This problem was asked by Triplebyte.

You are given n numbers as well as n probabilities that sum up to 1. Write a function to generate one of the numbers with its corresponding probability.

For example, given the numbers [1, 2, 3, 4] and probabilities [0.1, 0.5, 0.2, 0.2], your function should return 1 10% of the time, 2 50% of the time, and 3 and 4 20% of the time.

You can generate random numbers between 0 and 1 uniformly.

Step 1: Visualizing the Problem

This problem can seem slightly tricky at first. How can you generate random numbers with a fixed probability? How can we use what we’ve been given to solve this problem?

The first hint we’ve been given is that our probabilities will sum to one. This is the same range as the random number generator we are given. Therefore, we can map the probability to domains created by the number generator.

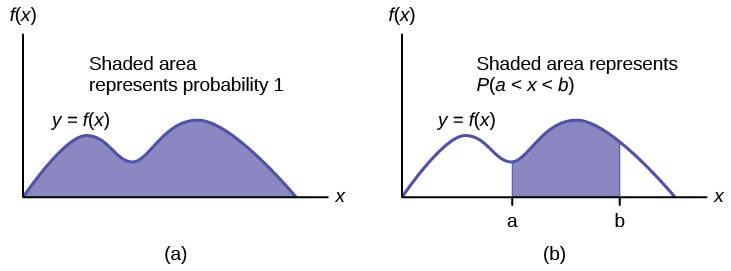
But what mapping should we use? Here is where some basic Math knowledge is helpful. One way to visualize probabilities is to sketch the probability distribution of the function. The probability of an event happening is the area of the region where the event happens. Look at the below image for a good visualization.

Visualization is a great technique that you should have in your problem-solving toolkit. I have a post dedicated to using visualization to create better solutions. You can find it below-

Using Visualization to create better solutions [Technique Tuesdays]

How does this apply to the question? We could imagine all the probabilities as distinct, disjoint intervals. For example, given the probabilities- [0.1, 0.5, 0.2, 0.2], you would get the intervals [0, 0.1), [0.1, 0.6), [0.6, 0.8), [0.8, 1]. Then we generate uniform random between 0 and 1 and select whichever value corresponding to the interval we fall in. That would look like this:

from random import random

def distribute(nums, probs):
    r = random() #our given 0-1 random number generator

    s = 0
    for num, prob in zip(nums, probs):
        s += prob
        if s >= r:
            return num

This would be an O(n) time and O(1) solution. Can we get any better than this? Yes and no. Technically speaking, no matter what we do, we will have an O(n) time complexity because we have to traverse the arrays to match our domains to the generated values. And we can’t go any lower than constant space. So what can we do?

This is where you really think like a software engineer. Let’s reread the problem, to really understand how we can improve the solution.

Step 2: Optimizing around the context

One interesting thing that the question tells us is that our function might be called multiple times. How do we know this? Remember the wording:

For example, given the numbers [1, 2, 3, 4] and probabilities [0.1, 0.5, 0.2, 0.2], your function should return 1 10% of the time, 2 50% of the time, and 3 and 4 20% of the time.

For a single run, we can’t get any better than our solution in Step 1. So what do we do? Let’s take a step back, and look at how we can make this generator more useful.

One thing to realize is that someone

But if we work in the fact that we might have multiple calls, then we see a problem. We will recreate identical spaces on every run. This is inefficient. Thus if we call this generator k times, our code will have the complexity of O(k*n) time complexity.

If we can build our list once, and just call our created generator a bunch of times, this would be much better. Since we are building probability ranges, we can build a range once, and binary search over it a bunch of times. To me, this idea resembles a cache, where we store the most common queries to speed up operations. A cache adds more overhead in the short term (in finding and storing the common instructions), but is amazing for performance in the long term.

Image Source

Our solution operates on the same principle. We build the range once and store it in memory. The subsequent look-ups become much cheaper because we don’t have to redo all the work from scratch.

Step 3: Coding It Up

The code for our newer variant looks like this-

from random import random
from bisect import bisect_left

def preprocess(probs):
    lst = []

    current_val = 0
    for p in probs:
        current_val += p
        lst.append(current_val)

    return lst

def distribute(nums, arr):
    r = random()
    i = bisect_left(arr, r)
    return nums[i]

def solution(nums, arr):
    times=int(input("Enter number of random numbers generated"))
    lst=preprocess(arr)
    ma={}
    for _ in range(times):
       rand=distribute(nums,lst)
       if rand not in ma:
           ma[rand]=1
       else:
            ma[rand]+=1
    #   print(rand) 
    print(ma)

solution([1,2,3,4],[0.1,0.5,0.2,0.2])   #testing our solution

To test this code out, we run this code 100,000 times we get:

Which is very close to what we want.

Time Complexity- O(n + k * log n) for k calls.

Space Complexity- O(n).

Loved the solution? Hate it? Want to talk to me about your crypto portfolio? Get my predictions on the UCL or MMA PPVs? Want an in-depth analysis of the best chocolate milk brands? Reach out to me by replying to this email, in the comments, or using the links below.

Stay Woke. I’ll see you living the dream.

Go kill all,

Devansh <3

Reach out to me on:

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd

Get a free stock on Robinhood. No risk to you, so not using the link is losing free money: https://join.robinhood.com/fnud75