[Solution]Problem 82: Find all the Bridges in a graph [Mozilla]

Graph Traversal, Graph Theory,DFS.

Hey, it’s your favorite cult leader here 🐱‍👤

On Thursdays, I will send you a problem + its solution. These solutions will help you reinforce your fundamental concepts, improve your problem-solving, and kill those Leetcode-Style Interviews. 🔥🔥💹💹

To get access to all my articles and support my crippling chocolate milk addiction, consider subscribing if you haven’t already!

p.s. you can learn more about the paid plan here.

---

Around 130,000 workers in U.S.-based tech companies (or tech companies with a large U.S. workforce) have been laid off in mass job cuts so far in 2023.

There’s a good chance some of you have been laid off/or are just generally struggling to find more work (I know it’s been rough for me). To help a little, I will be sharing some promising work that I come across that you can apply to.

The 2 Billion USD healthcare company, Hims&Hers is hiring a Senior Machine Learning Engineer (apply here). Here is some important information-

1. Base Salary- $125,000 - $175,000

2. Even though the JD is very machine learning heavy, they are not looking for AI-heavy devs (sadly for me 😢😢). Instead, they want software engineers with a lot of experience in backend engineering, who have some idea of Machine Learning.

3. The recruiter was kind enough to share the resume of an ideal candidate (one of their current employees) with me. You’ll find it here.

4. You can contact the recruiter- Nick- on LinkedIn here or through his email-  nflood@forhims.com

Feel free to reach out to him for any information, or just apply to the role at the link shared. Now onto the solution.

Problem

A bridge in a connected (undirected) graph is an edge that, if removed, causes the graph to become disconnected. Find all the bridges in a graph. Assume that the graph is finite

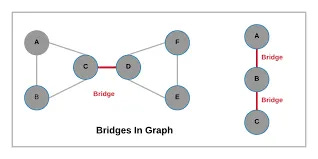
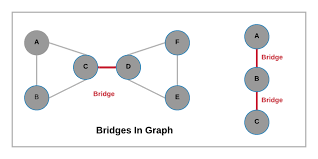
The above image is a good illustration of what bridges look like. For a formal definition, check out their Wikipedia.

Step 1: Understanding the Problem Nuances

Not everyone here has a background in graph theory. Therefore it is important to understand the minute details of the problem before rushing in. Once again let’s look at the following image shows us a graph and highlights the bridges.

Reading the definition of a bridge, you might notice something. If a node has only one edge, removing that edge disconnects the graph. And this will always hold true. So this must be a bridge, right?

This is where the question gets you. By trapping you a seemingly easy path, it can make you careless. It is true that if a node has only one edge, removing that will disconnect the graph. But…

, this is incomplete. It doesn’t imply the converse. Look at the following graph:

Here the graph has 3 bridges. (1,5) and (3,4) follow our previously established rule. But the rule missed (0,1) which is also a bridge. Sometimes, questions give you a seemingly simple way out, and many people carelessly go down that path. Don’t make that mistake.

So, how can we proceed?

Step 2: Brute Force Solution

As I’ve shown you many times, a good way to reliably create optimal solutions is to create the brute force solution and identify what makes the brute force inefficient. Our brute force looks like this-

To check if an edge is a bridge, all we have to do is remove the edge and check if the graph is connected (using a DFS/BFS). The procedure for this would look like this-

For every edge (u, v), do following:

1. Remove (u, v) from graph 

2. See if the graph remains connected (We can either use BFS or DFS). I recommend using DFS, since we are visiting every node anyway (and this graph is finite). The DFS will take up less memory. Check out this Technique Tuesday for more details on how to pick the right graph algorithm.  

3. Add (u, v) back to the graph.

The time complexity of the above method is O(E*(V+E)). This is because DFS/BFS all have a V+E time complexity and we repeat them E times.

For good practice, write the code out for this solution before proceeding. In your coding interviews, you only need to acknowledge this solution before proceeding to the more optimal solution.

So how can we optimize this?

Step 3: Working out the kinks (optimal soln)

Where does our Brute Force fail? Like with every other brute force solution, it wastes computations when it resets after every edge.

To solve this problem, we need to find some way to track which vertices are "reachable" from other vertices. Reachable is a graph theory concept. Node v is reachable from node u if we can somehow get to v from u using existing edges.

If we can manage this, we can identify an edge (u,v) as a bridge- if there does not exist any other alternative edge to reach u or an ancestor of u from subtree rooted with v. Removing (u,v) would separate v from the rest of the graph. In effect, we are identifying nodes that will be isolated if they weren’t connected to a single parent.

Now that we have the what, let’s move on to the how. How would we program our solution to find this?

Step 4: Thinking in DSA

As discussed already, performing a depth-first search is a good first step. Since we want to track which nodes we reach first, we need an array with the time of appearance of each vertex. If a vertex is explored on the first level of the search, appeared[v] = 0. For the second level, appeared[v] = 1, and so on. This tells us the ordering of the nodes.

At the same time, we store an array that holds the lowest level reachable from any vertex, which will initially be its own depth. For example, suppose we start our search with vertex 5 in the graph above. The value reach[5] initially will be 0. Next, we visit vertex 1, where we set reach[1] to 1. We continue our search in this way, increasing the depth at each step. When the stack eventually comes back to 1, reach[1] will be unchanged. In this way, we learn that it is impossible to form a path from 1 back to 0, and so (0, 1) must be a bridge.

Notice that since the graph is connected, it doesn’t matter where you start. Sure the specific value of reach[i] must be different, but the structure will stay the same. Take a second to verify this for yourself.

Now let’s wrap this up.

Step 5: Coding it Up.

Our solution looks like this-

def visit(graph, u, v, depth, reach, appeared, bridges):
    appeared[v] = reach[v] = depth

    for neighbor in graph[v]:
        if appeared[neighbor] == -1:
            visit(graph, v, neighbor, depth + 1, reach, appeared, bridges)

            if reach[neighbor] == appeared[neighbor]:
                bridges.append((v, neighbor))

            reach[v] = min(reach[v], reach[neighbor])

        elif neighbor != u:
            reach[v] = min(reach[v], appeared[neighbor])

def find_bridges(graph):
    reach = {v : -1 for v in graph}
    appeared = {v : -1 for v in graph}

    start = list(graph.keys())[0]
    depth = 0
    bridges = []

    visit(graph, start, start, depth, reach, appeared, bridges)

    return bridges

Time Complexity- O(V + E)

Loved the post? Hate it? Want to talk to me about your crypto portfolio? Get my predictions on the UCL or MMA PPVs? Want an in-depth analysis of the best chocolate milk brands? Reach out to me by replying to this email, in the comments, or using the links below.

Stay Woke,

Go kill all,

Devansh <3

Reach out to me on:

Small Snippets about Tech, AI and Machine Learning over here

Instagram: https://www.instagram.com/iseethings404/

Message me on Twitter: https://twitter.com/Machine01776819

My LinkedIn: https://www.linkedin.com/in/devansh-devansh-516004168/

My content:

Read my articles: https://rb.gy/zn1aiu

My YouTube: https://rb.gy/88iwdd