Understanding Big Oh, Big Theta, and Big Omega Notations[Math Mondays]

The different asymptotic complexity bounds are calculated.

May 16, 2023

Hey, it’s your favorite cult leader here 🐱‍👤

Mondays are dedicated to theoretical concepts. We’ll cover ideas in Computer Science💻💻, math, software engineering, and much more. Use these days to strengthen your grip on the fundamentals and 10x your skills 🚀🚀.

To get access to all the articles and support my crippling chocolate milk addiction, consider subscribing if you haven’t already!

Help me buy chocolate milk

p.s. you can learn more about the paid plan here.

This is one of the most common questions that a lot of people deal with.

Whether you’re a student trying to pass your algorithms course, a developer trying to pass your Leetcode interviews, or a professional trying to estimate costs- this is a topic that will show up frequently. It is also one of the most requested topics in this newsletter. So I figured I’d do an overview of the different kinds of notation you will see in complexity calculations and software engineering.

Exploring the Tech Domain, one meme at a time

Asymptotic Complexity 101

What is time complexity- Counter-intuitively. time complexity calculations have nothing with the time it would take to run your code. This is because things like hardware can have a drastic impact on the seconds you need to run your code. Instead, the time complexity of your algorithm refers to the number of instructions your software will execute prior to completion. Measures like Big Oh are just measures of this.
Types of Algorithmic Complexity- There are three asymptotic notations typically used to compute time complexity. This article by Geeks For Geeks is a great summary of it.
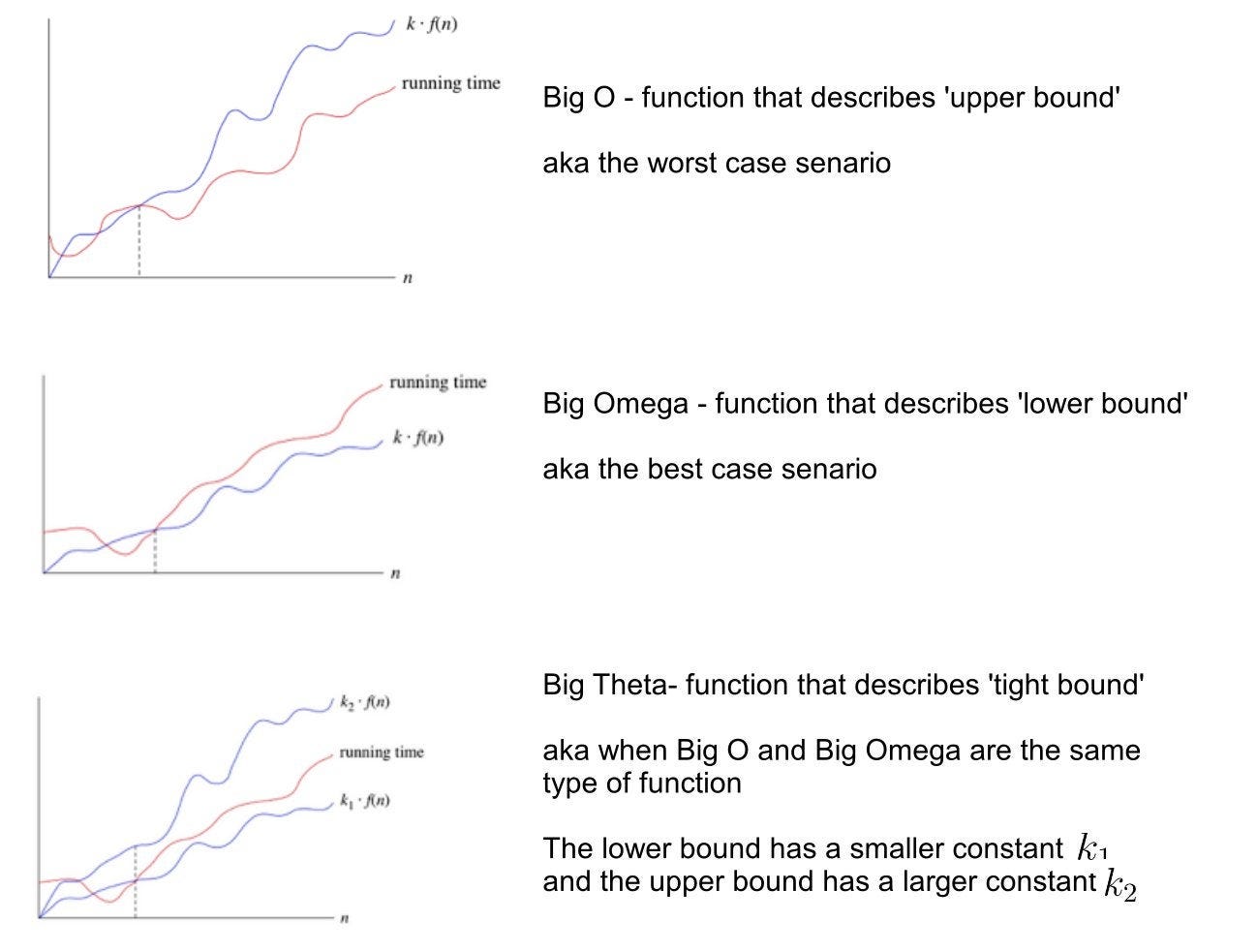
- Big O (O): This notation is used to describe an upper bound on the running time of an algorithm. In other words, it is the fastest that an algorithm can run, no matter what the input size is. Mathematically, if f(n) describes the running time of an algorithm; f(n) is O(g(n)) if there exist positive constant C and n0 such that,
  0 <= f(n) <= Cg(n) for all n >= n0
  n = used to give upper bound an a function.
- Big Omega (Ω): This notation is used to describe a lower bound on the running time of an algorithm. In other words, it is the slowest that an algorithm can run, no matter what the input size is. Let f(n) define the running time of an algorithm; f(n) is said to be Ω(g (n)) if there exists positive constant C and (n0) such that
  0 <= Cg(n) <= f(n) for all n >= n0
  n = used to given lower bound on a function
- Big Theta (Θ): It is defined as the tightest bound- the best of all the worst-case times that the algorithm can take. Think of it as the most precise bounding of the bunch.
- If you like images, this is a great visualization-
The most common bounds- In the wild, you will come across the following types of bounds very frequently-
- Constant time: The algorithm costs grow at a constant pace.
- Logarithmic time: The costs are proportional to the logarithm of the size of the input.
- Linear time: The costs grow proportional to the size of the input.
- Quadratic time: The costs grow proportional to the square of the size of the input.
- Exponential time: The costs grow proportional to the power of the size of the input. You will typically not see anything beyond this. If you have seen factorial time complexity in your work, I’d love to hear about it.
Image Source

Time complexity bounds are one of the few concepts from theoretical computer science that you will see regardless of what you’re working on. Master them really well. We will do a separate post on the data structures and the costs associated with them soon.

That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. If you like my writing, I would really appreciate an anonymous testimonial. You can drop it here. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow.

Save the time, energy, and money you would burn by going through all those videos, courses, products, and ‘coaches’ and easily find all your needs met in one place at ‘Tech Made Simple’! Stay ahead of the curve in AI, software engineering, and the tech industry with expert insights, tips, and resources. 20% off for new subscribers by clicking this link. Subscribe now and simplify your tech journey!

Using this discount will drop the prices-

800 INR (10 USD) → 640 INR (8 USD) per Month

8000 INR (100 USD) → 6400INR (80 USD) per year (533 INR /month)

Get 20% off for 1 year